What are the forces acting on a stationary block with strings pulling on it?

[caela]

Hi Guys,

Having a super hard time with this homework question. I've done similar problems, but the fact that the box is ON the ground and not suspended is confusing me.

Quoted from my book:
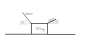
"Two strings are pulling on a 50-kg block as shown. The block does not move. The coefficient of static friction between the floor and the block is µs=0.6
A. Find the magnitude of the normal force exerted by the floor on the block.
B. Find the magnitude of the static friction force exerted by the floor on the block."

http://tinypic.com/r/28kisrk/6
(The left string is 200 N with an angle of 53 degrees, and then right string is 100 N with an angle of 37 degrees, I know it's a little hard to read)

Thanks so much for any help! :)

 

[PhysicsMark]

Hi. I would think of the components of the tensions in each string that are opposing the force of gravity...(100N*sin(37) is one of them)

 

[caela]

Ok, so if I add up the two y values: 200cos(53) + 100cos(37) = 180
Then subtract the force of the box from the y values? 500 N-180 N = 320 N

And then for static friction, I would multiply 320 * .6 = 192?

It seems suspiciously easy...

 

[PhanthomJay]

Confirming your suspicion, nothing in Physics is particularly easy. You have calculated the Normal force correctly. You must now look in the x direction to get the friction force.