What are the forces on a hinged beam supporting a shop sign?

[djunderseage]

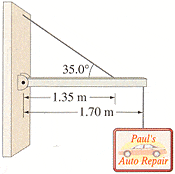
A shop sign weighing 255 N is supported by a uniform 145 N beam as shown in Fig. 9-54. Find the tension in the guy wire. Find the horizontal and vertical forces exerted by the hinge on the beam.

 

[fluidistic]

Write down all the forces acting on the system. The system is in static equilibrium so what can you conclude from it? (Meaning about the torque and sum of all forces).

 

[djunderseage]

i have that done just didnt know how to put it on the forum. i think they would be 0...

 

[fluidistic]

Right. Now solve the equations you have. Especially solve for what they're asking you.