stinlin
- 72
- 1
Homework Statement
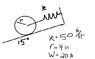
W = 20 lb
k = 50 lb/ft
r = 4 in.
Initially displaced 0.5 in.
Determine the frequency and maximum velocity of the wheel (which rolls without slipping).
Homework Equations
(theta) double dot + (w^2)theta = 0
(x) double dot + (w^2) (x) = 0
t = 2*pi / w
The Attempt at a Solution
I wrote out the initial information. The amplitude is 0.5 in. I didn't know which equation to use (the one with theta or with x). But I used the one with x and wrote out the moment balance and force balance, only to find that I was off.
I thought to use the theta equation, but I cannot figure out where to go with it. I know alpha = theta double dot. x = r(theta), but I don't know where to go from that either.
Any help and direction would be awesome! I have 2 other problems, but just understanding this one might get me going on the others.