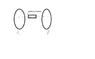What are the Induced Poles in Coaxial Coils Facing a Moving Bar Magnet?

Click For Summary
SUMMARY

The discussion centers on the behavior of induced poles in two coaxial coils, A and B, when a bar magnet is moved between them. It is established that coil A will induce a south pole to oppose the approaching north pole of the magnet, while coil B will also induce a south pole to attract the magnet. This phenomenon is a direct application of electromagnetic induction principles, specifically Lenz's Law, which states that the direction of induced current (and thus the induced magnetic field) will oppose the change in magnetic flux.

PREREQUISITES
  • Understanding of electromagnetic induction principles
  • Familiarity with Lenz's Law
  • Basic knowledge of magnetic fields and flux
  • Concept of coaxial coils and their configurations
NEXT STEPS
  • Study Lenz's Law in detail to understand its applications
  • Explore the concept of magnetic flux and its directionality
  • Investigate the behavior of coaxial coils in various magnetic field scenarios
  • Learn about Faraday's Law of electromagnetic induction
USEFUL FOR

Students of physics, educators teaching electromagnetism, and anyone interested in the practical applications of electromagnetic induction in coil systems.

pratyushag
Messages
12
Reaction score
0

Homework Statement


A bar magnet is moved between 2 coaxial coils A and B as shown in the figure.The end planes of the two coaxial coils facing the magnet due to induction will behave?


Homework Equations





The Attempt at a Solution



My solution:
It will induce south pole in A and B
south pole in A as the coil needs to oppose the magnet
south pole in B because the coil needs to attract the magnhet

(I have read these properties in a book,so I am just applying them but I don't know what's the logic behind them)
 

Attachments

  • physics2.png
    physics2.png
    4 KB · Views: 602
Physics news on Phys.org
pratyushag said:

Homework Statement


magnetic flux have definite direction and they never cross path, always from North to South forming a complete closed loop. think about it.
 

Similar threads

Lenz' law: North pole of bar magnet moves away from a coil
  • · Replies 10 ·
Replies
10
Views
2K
High School EMF induced by Bar Magnet falling through a Coil
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad How induction works within a coil (nuances of it)
  • · Replies 6 ·
Replies
6
Views
2K
Electromagnetic induction questions
  • · Replies 2 ·
Replies
2
Views
3K
Magnet moved in a circular coil
  • · Replies 10 ·
Replies
10
Views
2K
Deduction about Magnetic Poles surrounding a Conductor
  • · Replies 40 ·
2
Replies
40
Views
3K
Induced current of a coil on another coil
  • · Replies 6 ·
Replies
6
Views
5K
Force in a magnetic field on a moving coil
  • · Replies 5 ·
Replies
5
Views
2K
Electromagnetic Induction Problem (Very Introductory)
  • · Replies 3 ·
Replies
3
Views
5K
Effects of Reversing Magnet Motion on Induced Current and Magnetic Field
  • · Replies 7 ·
Replies
7
Views
2K