What Are the Initial Speeds of Two Cars After a Rear-End Collision?

[Nikolan]

Homework Statement

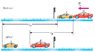
In the "before" part of Fig. 9-60, car A (mass 1100 kg) is stopped at a traffic light when it is rear-ended by car B (mass 1500 kg). Both cars then slide with locked wheels until the frictional force from the slick road (with a low μk of 0.21) stops them, at distances dA = 5.3 m and dB = 3.4 m. What are the speeds of (a) car A and (b) car B at the start of the sliding, just after the collision? (c) Assuming that linear momentum is conserved during the collision, find the speed of car B just before the collision.

(see attachment for image)

Homework Equations

(A = CarA, B = CarB)

PAi + PBi = PAf + PBf
(mA)vAi + (mB)vBi = (mA)vAf + (mB)vBf

The Attempt at a Solution

I've been sitting here looking blankly at this problem for about an hour now. I really have no idea where to start with this, I've tried a few things, but it always ends up giving me two unknown variables. Looking at another thread that was posted on this question, I realize that all the kinetic energy is transferred to thermal in the end, how does that help?

(https://www.physicsforums.com/showthread.php?t=82429)

 

[lanedance]

Hi Nikolan, welcome to PF

For a) & b) think about one car at a time. After the collision, the work done by friction slowing the car will equal the decrease in kinetic energy of the car.

 

[Nikolan]

Thank you very much!

I ended up taking what you said and applying it like this:

(Using this solution for both cars A and B)

Fk = (uk)FN to find force of friction.

W of Friction = (Fk)(D) = Kf - Ki = 1/2mvf^2 - 1/2mvi^2

to get:

W = - 1/2mvi^2 => sqrt(((-2)(W))/M) for initial speeds of both cars directly after impact.
I then used Momentum of Cars before = Momentum afterwards
or
Pai + Pbi = Paf + Pbf
mavai + mbmbi = mavaf + mbvbf

and plugging in relevant values to end up with initial speed of car B before collision.Again, thanks for your help!