What Are the Possible Loci When d (x, y) = max {|x|,|y|}?

[Saitama]

Homework Statement

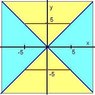
If the distance of any point (x,y) from the origin is defined as
d (x, y) = max {|x|,|y|},
d (x, y) = a non zero constant, then the locus is

(a) a circle
(b) a straight line
(c) a square
(d) a triangle

Homework Equations

The Attempt at a Solution

I don't understand what does the question mean by "d (x, y) = max {|x|,|y|}"?

Can somebody tell what does the notation mean? I never encountered problems like these.
Any help is much appreciated.

Thanks!

 

[phinds]

what do you understand of the various symbols used?

What does "|x|" mean, for example

If you have no idea what the symbols mean, one has to wonder what you are doing working on the problem with no background, but if you do understand them, then say what they are and see where that leads.

 

[Saitama]

what do you understand of the various symbols used?

What does "|x|" mean, for example

If you have no idea what the symbols mean, one has to wonder what you are doing working on the problem with no background, but if you do understand them, then say what they are and see where that leads.

I know what does |x| mean. My question is what does this "max" and "d(x,y)" mean?
(x,y) are the co-ordinates of a point but i don't understand what this "d(x,y)" mean.

Thanks for the reply!

 

[ehild]

d(x,y) is just a function, it is not the same as the classical distance. It is defined as max(|x|,|y|), so d=|x| when |x|>|y| and d=|y| when |y|>|x|. Find the locus where d(x,y)= constant. Draw a picture of the coordinate system and find the regions where |y|>|x| and |x|>|y|. Draw the lines d=const. You will see the solution at once.

ehild

 

[Saitama]

d(x,y) is just a function, it is not the same as the classical distance. It is defined as max(|x|,|y|), so d=|x| when |x|>|y| and d=|y| when |y|>|x|. Find the locus where d(x,y)= constant. Draw a picture of the coordinate system and find the regions where |y|>|x| and |x|>|y|. Draw the lines d=const. You will see the solution at once.

ehild

I drew the graph of the both |x| and |y| on the same graph and found that the graphs of both |x| and |y| coincides with each other.
Is the coinciding line is my answer?

 

[ehild]

I drew the graph of the both |x| and |y| on the same graph and found that the graphs of both |x| and |y| coincides with each other.
Is the coinciding line is my answer?

NO. Show your drawing, please. You need to find those points in that domain of the x,y plane where |y|>|x| for which d(x,y)= |y| =const, for example d(x,y) = |y|=5. And also find those points (x,y), |x|>|y|, for which d(x,y)=|x|=5

ehild

 

[Saitama]

NO. Show your drawing, please. You need to find those points in that domain of the x,y plane where |y|>|x| for which d(x,y)= |y| =const, for example d(x,y) = |y|=5. And also find those points (x,y), |x|>|y|, for which d(x,y)=|x|=5

ehild

My graph is similar to this:- http://www.wolframalpha.com/input/?i=|y|=x,y=|x|

 

[ehild]

The plot is a good start to show the domains, but complete it for x<0, y<0. Then draw the line(s) |y|=5 in the range |x|<|y|.ehild

 

[Saitama]

The plot is a good start to show the domains, but complete it for x<0, y<0. Then draw the line(s) |y|=5 in the range |x|<|y|.


ehild

Here's the graph which i drew (Not to scale):-

|y|=5, that mean y=5 or y=-5, i draw both of them but i still don't understand what you mean by |x|<|y|?

Sorry if this is annoying for you.

 

[ehild]

The lines y=5 and y=-5 do not extend to infinity. d(x,y)=max(|x|,|y|)=5. It is equal to |y| while |y|>|x|, in the yellow area of the x,y plane. In the blue area, where |x|>|y|, d(x,y)=5=|x|. Draw it.

ehild

 

[I like Serena]

Hi Pranav!

Perhaps you could consider a few points in the plane.
Like (x=1, y=5), (-4,5), (-6,5), (1,1), (-5,4), (-5,-4), (-3,-5).
Can you say what max(|x|,|y|) is in each case?