What are the tensions in strings 2 and 3 and the acceleration of the mass?

[Mivz18]

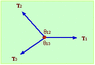
Problem : Three strings, in the horizontal plane, meet in a knot and are pulled with three forces such that the knot is held stationary. The tension in string 1 is T1 = 2.5 N. The angle between strings 1 and 2 is q12 = 130° and the angle between strings 1 and 3 is q13 = 120° with string 3 below string 1 as shown.

a) Find the tension in string 2.
b) Find the tension in string 3.

A mass of 1.2 kg is now placed on the knot and supported by a frictionless table in the plane of the strings.

c) Find the acceleration of the mass if all the forces remain the same as above.
d) If the sizes and directions of T2 and T3 remain the same, but T1 is increased by 1.5 N, what is the acceleration of the mass?

Ok, first I decompose the tensions into their x and y components. After substitutions and combining equations, I end up with these final equations.

T2x = T2(cos 130)
T2y = T2(sin 130)
T3x = T3(cos (-120))
T3y = T3(sin (-120))

I can then put the formulas in a cartesian coordinate system:

(2.5 + T2(cos 130) + T3(cos -120) ) , (T2(sin 130) - T3(cos -120) ) = (0,0)

2.5 + T2(cos 130) + T3(cos -120) = 0
T2(sin 130) - T3(cos -120) = 0

T2 = (T3(sin -120)) / Sin(130)

When setting the two equations equalling zero to each other, I substituted the previous for T2. Then when solving for T3 I get 1.533 N.

Am I doing this correctly because the program I am using says that is incorrect and I am stuck.

 

[arildno]

Here, it seems you have mixed sin and cos:
"T2(sin 130) - T3(cos -120) = 0

T2 = (T3(sin -120)) / Sin(130)
"

 

[Mivz18]

Well, I fixed my sin, cos error, but my answer of 2.1688 is still incorrect. Any suggestions?

 

[Doc Al]

I can then put the formulas in a cartesian coordinate system:

(2.5 + T2(cos 130) + T3(cos -120) ) , (T2(sin 130) - T3(cos -120) ) = (0,0)

The x coordinate is OK; the y coordinate, is wrong: in addition to the sin/cos mixup, you subtracted the components instead of adding them.

 

[arildno]

I'm sorry I mislead you!
The vertical equation is of course:
T_{2}\sin(130)+T_{3}\sin(-120)=0
That is:
T_{2}=T_{3}\frac{\sin(120)}{\sin(130)}
(This is distinct from your own, original expression!)
I'll check if I find any more errors lurking about..

 

[Mivz18]

Ok, I changed my sin, cos errors and the y component equation to :

T2 (sin 130) + T3 (cos -120) = 0

This in turn creates T2 = - (equation). I solve and something still seems incorrect. Is there an error still lurking somewhere?

 

[Mivz18]

Can anyone help me solve this problem? Physics is like a foreign language to me now.

 

[Doc Al]

Ok, I changed my sin, cos errors and the y component equation to :

T2 (sin 130) + T3 (cos -120) = 0

Still wrong. Change that cosine to a sine! (See arildno's last post.)

 

[Mivz18]

THANK YOU SOOO VERY MUCH! I finally got it!