What Does A=0 or S=-3/2 Indicate in Laplace Transform Analysis?

[baby_1]

Laplace Error in a Circuit !

Hello
as you see this circuit

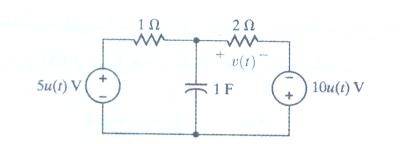
i want to find the v(t) across the 2ohm resistor.(VC(0-)=0)
i assume A node above the capacitor , so we have (in Laplace)

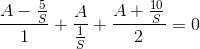
so i have

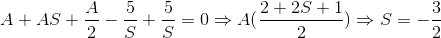
so A=0 ! or S=-3/2 ! what can we understand about A=0 or S=-3/2 ? what is their inverse Laplace in time zone?

now how can find the v(t) across the 2ohm resistor? Thanks

 

[baby_1]

Hello Again
i have a new question about above circuit. now how can find the voltage across the capacitor?

 

[thegreenlaser]

What's wrong with A=0? That just means there's no voltage drop across the capacitor, so finding the voltage across the resistor should be pretty straight forward. Also, you shouldn't call s=-3/2 a solution, because your node equations should hold for all values of s. The only way your node equation holds for all values of s is when A=0. Hence, the voltage across the capacitor (A) is zero.

Admittedly this is a bit of an odd circuit. Here's two things you can do to try to understand.

1. Replace the 5/s source with an arbitrary source V1(s) and replace the 10/s source with an arbitrary source V2(s). Solve for A(s) in terms of V1(s) and V2(s). You should see that when V2 = 2*V1 (as is the case here), A(s) goes to zero, but if not A(s) will have an exponential response like you would normally expect. Essentially, in this case the sources are perfectly balanced so that they don't charge up the capacitor. If you had a 5/s source and a 15/s source, the capacitor would charge up to some value and A(s) wouldn't be zero.

2. Look at the steady state response. What would you expect the voltage on the capacitor to be as t goes to ∞? The capacitor is starting at zero volts, and then charging up to this value. Can you see why the voltage on the capacitor would stay constant at zero?

 

[baby_1]

Hello dear thegreenlaser
Thanks a lot for you explanation
i want to know the laplace give us the steady state value of the circuit?

 

[thegreenlaser]

Have you studied steady state values at all? In this case you would assume the capacitor acts like an open circuit at t=∞, so you would replace the capacitor with an open circuit and find the voltage across it. If you've never seen anything like that before, then don't worry about it. I was just trying to give you another way to get an intuitive feel for what's going on.

To answer your question about using Laplace, there is indeed a way to find steady state values directly from your Laplace expression. It's called the final value theorem, but the theorem doesn't really offer much in the way of understanding why the final value should be what it is. In this case, I think the final value theorem would just make things more confusing.

 

[baby_1]

Thanks thegreenlaser again for your best explanation
could you tell me how can we know we have a Jump capacitor voltage with laplace ?for example VC(0-)<> VC(0+)?

 

[aralbrec]

Thanks thegreenlaser again for your best explanation
could you tell me how can we know we have a Jump capacitor voltage with laplace ?for example VC(0-)<> VC(0+)?

An impulse would do it.

 

[baby_1]

thanks dear aralbrec
could you tell my how can find we have a jump in capacitor voltage without impulse source?

Thanks

 

[aralbrec]

could you tell my how can find we have a jump in capacitor voltage without impulse source?

You can view an initial capacitor voltage as an impulse. Follow the Laplace transform:

i = C dv/dt

I(s) = sC V(s) - Cv(0-)

This says you can model the current through the capacitor as an uncharged capacitor with an impulse current source in parallel. The impulse source places the initial voltage on the capacitor at t=0. Vi = Q/C = ∫i dt / C = Cv(0-)/C = v(0-)

Normally we manipulate the equation a little further:

V(s) = I(s) /(sC) + v(0-)/s

which says the capacitor can be modeled as an uncharged capacitor in series with a constant voltage source.