What does Griffith mean by this hint? [Electrodynamics]

[Mind----Blown]

I was solving the problems given by Griffith in his book 'Introduction to Electrodynamics' and stumbled across this question.

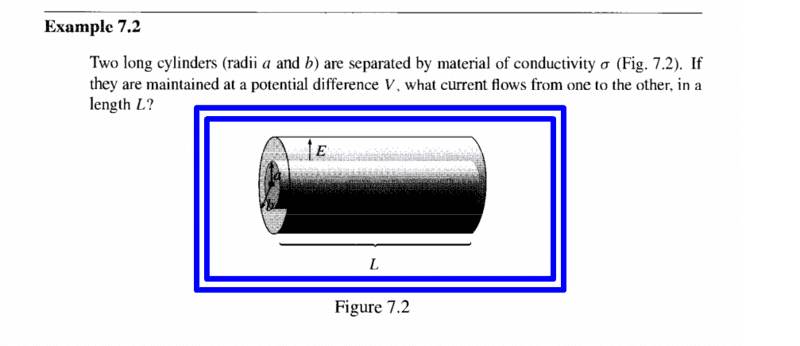
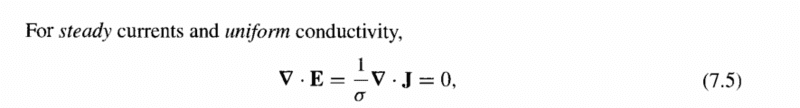
"Because sigma (conductivity of the medium) is a function of position, the equation 7.5 does not hold" --i get this point; current density isn't constant and so its divergence will be non zero.
"The charge density is non zero in the resistive medium"-- I have no clue what this sentence means.. I can't even think why i don't find it right.. someone please explain it to me!

Thanks a lot !

 

[vanhees71]

Another hint: Use the constitutive equation
$$\vec{j}=\sigma \vec{E}$$
and the continuity equation for stationary currents
$$\vec{\nabla} \cdot \vec{j}=0,$$
which together immediately tell you, how to modify Eq. (7.5). Also it would be helpful to tell, what $s$ is. Is it the cylinder coordinate $r$ in standard notation? I guess so from the Figure, which indicates that $\vec{E}$ is radially out.

PS: Questions like this should be posted in the homework forum!