Mrhu
- 7
- 0
Homework Statement
Hello again!
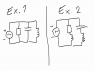
We have been given a couple of more advanced problems where the components are placed in series parallely.
Check the image, the question is regarding what equation to use, in order to calculate the total impedance of the circuit.
Homework Equations
I have stumbled upon the following equations...
Z_{tot}=\frac{1}{\frac{1}{Z_{1}}+\frac{1}{Z_{2}}}
And the same equation, only squared and partly modified
Z_{tot}=\frac{1}{\sqrt{(\frac{1}{R})^{2}+(\frac{1}{X_{L}}-\frac{1}{X_{C}})^{2}}}
The Attempt at a Solution
If you take a look at the image you will see two examples, my theory is that the second equation is valid for the first example.
But when does one use the first equation? And can the second equation be used on the second example, and vice versa?
Many thanks in advance, please do use real numbers when explaining. I am aware of the importance of complex numbers in RLC circuits we have not applied them in Physics yet.