eddiepi2012
- 6
- 0
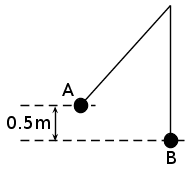
1.2. If a ball and string pendulum is pulled and lifted to a height = 10 cm and the length of the string is 1 m what will be the value of h when the string makes an angle of 90 degree with the vertical? Please ignore the 0.5 m it should be a h = 10 cm or 0.1 m the diagram is to provide a description of how this question is worded.
2.c2 = a2 + b2 = b2 = c2 – a2, T sin theta – mg = 0
3. 1 m – 0.1 m = 0.9 m
c2 = a2 + b2 = b2 = c2 – a2
b2 = 12 – 0.92
b2 = 1 – 0.81
b2 = 0.19
b = √(0.19) = 0.4
= cos-1 (0.4) = 66 degrees
2.c2 = a2 + b2 = b2 = c2 – a2, T sin theta – mg = 0
3. 1 m – 0.1 m = 0.9 m
c2 = a2 + b2 = b2 = c2 – a2
b2 = 12 – 0.92
b2 = 1 – 0.81
b2 = 0.19
b = √(0.19) = 0.4
= cos-1 (0.4) = 66 degrees
Last edited: