fwFAWFSERG
- 11
- 0
1. i have the answer, but just don't understnad it
A small metal ball is given a negative charge, then brought near (i.e., within a few millimeters) to end A of the rod. What happens to end A of the rod when the ball approaches it closely this first time?
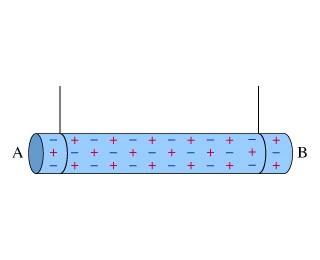
Select the expected behavior.
X strongly repelled
X strongly attracted
weakly attracted
X weakly repelled
X neither attracted nor repelled
Well, i first figured that the negatively charged ball and the side A of the rod would weakly repel, seeing that there are two negative charges, and one postive charge, a ratio of 2:3 negative.
-that answer was wrong
then i thought that since it was an insulator, and is not even really charged (having a nuetral charge as a whole) it would be neither attracted nor repelled.
-also wrong.
-so, an insulator does not transfer charge well, but i don't see how this helps me answer the question really.
so it's weakly attracted because the insulator rearranges to give a small dipole moment, which makes it weakly attracted?
A small metal ball is given a negative charge, then brought near (i.e., within a few millimeters) to end A of the rod. What happens to end A of the rod when the ball approaches it closely this first time?
Select the expected behavior.
X strongly repelled
X strongly attracted
weakly attracted
X weakly repelled
X neither attracted nor repelled
The Attempt at a Solution
Well, i first figured that the negatively charged ball and the side A of the rod would weakly repel, seeing that there are two negative charges, and one postive charge, a ratio of 2:3 negative.
-that answer was wrong
then i thought that since it was an insulator, and is not even really charged (having a nuetral charge as a whole) it would be neither attracted nor repelled.
-also wrong.
-so, an insulator does not transfer charge well, but i don't see how this helps me answer the question really.
so it's weakly attracted because the insulator rearranges to give a small dipole moment, which makes it weakly attracted?
Last edited: