You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
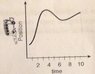
The discussion focuses on understanding the relationship between position (x(t)) and velocity (v(t)) of a bus over time. It explains that velocity is determined by the change in position over time, with specific cases where the bus's velocity is zero or negative. A horizontal position graph indicates zero velocity, while a steep slope suggests high velocity. The conversation emphasizes the importance of analyzing the slope of the position versus time graph to determine the bus's velocity at different intervals. Overall, the key takeaway is that velocity reflects both speed and direction, with graphical analysis being crucial for understanding motion.
Physics news on Phys.org
Villyer
- 294
- 0
What do you know about the relationship between x(t) and v(t)?
saalrom
- 2
- 0
I know that V = (Xf-X1)/T, and that x represents the location of an object and t represents time. V represents velocity.
Spaghetti
- 3
- 0
The graph in your problem is showing the position of the bus as time passes.
Think about how the position is changing as time moves on, or possibly over specific intervals of time.
Imagine the position line was going across the graph completely horizontally. That would mean the position isn't changing, so the bus must have no velocity.
Now think about if the position changed greatly over a very small period of time. Since the position is changing very quickly, the bus must be moving very quickly.
And remember that velocity is just speed with a direction. If an object is moving forward at 60 miles per hour, that object has a speed of 60 miles per hour, and a positive velocity of 60 miles per hour. If that same object is then going in the opposite direction (backwards) at 60 miles per hour, that object has a speed of 60 miles per hour, and a negative velocity of 60 miles per hour.
Is there a specific part of the problem you're having trouble with? With just the problem and no thoughts with it, it's a bit difficult to figure out where you're at!
Villyer
- 294
- 0
Has any graphical analysis of the graph of x(t) been mentioned before?
For example, what does the slope of a position v. time graph tell you?
azizlwl
- 1,066
- 10
Take a point on the graph.
Take second point which is right to the 1st. point as close as possible.
If point #2>(higher)point #1 then velocity positive
If point #2=point #1 then velocity zero
If point #2<(lower)point #1 then velocity negative
Hello guys this is what I tried so far. I used the UTS to calculate the force it needs when the rope tears.
My idea was to make a relationship/ function that would give me the force depending on height. Yeah i couldnt find a way to solve it.
I also thought about how I could use hooks law (how it was given to me in my script) with the thought of instead of having two part of a rope id have one singular rope from the middle to the top where I could find the difference in height.
But the...
Here is what I tried
This question was actually asked in one of our engineering entrances.
The answer was 1D.
My teachers say that we have to use μₘ/fₘ to get to this answer. I cannot understand why. I'll be really glad if you could tell me the exact definition of power (numerically) that works in all scenarios.
TL;DR Summary: I would like to know the voltmeter readings on the two resistors separately in the picture in the following cases , When one of the keys is closed When both of them are opened (Knowing that the battery has negligible internal resistance)
My thoughts for the first case , one of them must be 12 volt while the other is 0
The second case we'll I think both voltmeter readings should be 12 volt since they are both parallel to the battery and they involve the key within what the...
Similar threads
- Replies
- 8
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 13
- Views
- 1K
- Replies
- 22
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 9
- Views
- 1K
- Replies
- 29
- Views
- 3K
- Replies
- 60
- Views
- 4K
- Replies
- 2
- Views
- 732
- Replies
- 2
- Views
- 892
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 3
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 29
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math