What is permanent magnet B field equation?

AI Thread Summary
To calculate the magnetic field (B) between two permanent magnets positioned 10mm apart, with each magnet having a core intensity of 1.3T and a surface intensity of 0.6T, one can use the formula for the electric field (E) due to a uniformly charged disk, as the B field behaves similarly under certain conditions. The B field at a distance of 5mm from the face of one magnet can be approximated as the sum of the fields from both magnets, effectively doubling the value. For precise calculations, it is essential to consider the dimensions of the magnets and their respective intensities. The relevant formula can typically be found in standard physics textbooks. This approach provides a basis for calculating the magnetic intensity between the magnets at the specified distance.
ShahinPhD
Messages
2
Reaction score
0
I'm looking for an equation to calculate Tesla (B) between two permanent magnets with distance of 10mm.

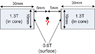
Magnets are located in front of each other; disk shape and intensity of each is 1.3T in its core, and 0.6T on surface, so I'm interested how to calculate the B between them in distance of 5mm from each one (10mm between 2 magnets).

Please help me to find proper calculation.
Thanks in advanced.
 
Physics news on Phys.org
If the magnets are much longer than 5mm, the B field 5mm from the face of one magnet is the same as the E field 5mm from a uniformly charged disk with charge density
\sigma=M where M=13,000 gauss (all in Gaussianl units). Just double it for two magnets.
 
Thanks for your fast response.
It seems OK, but in a short form I'm looking for a formula to calculate the Tesla in distance between two magnets.
Suppose we have some parameters: dimensions of magnets, power of magnets in core and surface, distance between them; so how can we use a formula to calculate intensity between magnets in some distance?

(Frankly I'm looking for a formula to use for my calculations)
 

Attachments

  • magnet.gif
    magnet.gif
    4.6 KB · Views: 548
The on axis formula for E due to a uniformly charged disk is in most (even elementary) textbooks.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Does levitation distance increase as Fg increase???
Replies
1
Views
912
Does a Bent Wire Affect Induction Calculations?
Replies
7
Views
2K
(Magnetism) Magnetic pull force on a steel ball
Replies
4
Views
2K
Finding magnetic field using Ampere's Circuital Law
Replies
5
Views
982
Understanding work in translation and rotation of a magnetic dipole
Replies
1
Views
2K
Spring-mediated dipole in a magnetic field
Replies
31
Views
2K
How to Find the Magnetic Field (B) in a Zeeman Effect
Replies
3
Views
1K
Derivation Of Torque On Current Loop Due To Uniform Magnetic Field
Replies
4
Views
2K
Motional EMF in the presence of a time-varying magnetic field
Replies
11
Views
3K
Finding the magnetic field at a point
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top