primarygun
- 233
- 0
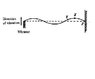
1.In the figure, describe the motion of particles X and Y at the instant.
What will be the shape of the string after 1/4 cycle?
I don't know which direction that the crests are traveling as there are two sources.
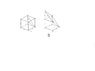
2.The tetrahedron BCDH is cut off from the cube and is then placed on top of the solid ABDEFGH as shown in the figure. The face BCD of the tetrahedron coincides with the face BAD of the solid ABDEFGH such that vertex H of the tetrahedron moves to the position of V and vertex C coincides with A. The faces BHD and BVD of the new solid lie on the same plane.
What's the projection of point F on the plane BDH?
What will be the shape of the string after 1/4 cycle?
I don't know which direction that the crests are traveling as there are two sources.
2.The tetrahedron BCDH is cut off from the cube and is then placed on top of the solid ABDEFGH as shown in the figure. The face BCD of the tetrahedron coincides with the face BAD of the solid ABDEFGH such that vertex H of the tetrahedron moves to the position of V and vertex C coincides with A. The faces BHD and BVD of the new solid lie on the same plane.
What's the projection of point F on the plane BDH?