What Is the Angle of the Rod in the Magnetic Field?

[Dart82]

1. Homework Statement
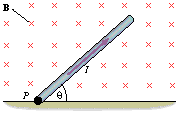
a thin, uniform rod, which has a length of 0.45 m and a mass of 0.080 kg. This rod lies in the plane of the paper and is attached to the floor by a hinge at point P. A uniform magnetic field of 0.25 T is directed perpendicularly into the plane of the paper. There is a current I = 3.8 A in the rod, which does not rotate clockwise or counter-clockwise. Find the angle .

2. Homework Equations
F = ILB sin(theta)
F= ma


3. The Attempt at a Solution
heres what i was thinking:
if F = ILB sin(theta) then let ma = ILBsin(theta)

so solve for theta:
arcsine(ILB/ma) = 33.0 degrees however, i was told this is wrong.

 

[Dick]

Do the magnetic and gravitational forces act in the same direction? Hint: no. Draw a force diagram.

 

[Dick]

Also, is the theta in your picture the same as the theta in the B equation? Hint: no.

 

[Dart82]

thanks for the help. i think it got it finally.