What is the Angular Momentum of a System with Pulleys and Blocks?

[postfan]

Homework Statement

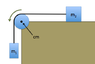
A block of mass m1 is attached to a block of mass m2 by an ideal rope passing over a pulley of mass M and radius R as shown. The pulley is assumed to be a uniform disc rotating freely about an axis passing through its center of mass (cm in the figure). There is no friction between block 2 and the surface. Assume that the pulley rotates counterclockwise as shown with an angular speed ω and that the rope does not slip relative to the pulley, and that the blocks move accordingly and do not topple or rotate.

Consider the system to be formed by the pulley, block 1, block 2 and the rope.

Calculate the magnitude of the angular momentum of the system about the center of mass of the pulley. Express your answer in terms of some or all of the variables m1, m2, M, R, ω and g. Type omega for ω

Homework Equations

The Attempt at a Solution

Used formula L=Iw I=.25MR^2 then multiply by w so L=1/4*(M*R^2)*w. What am I doing wrong?

 

[TSny]

Is there any way you can post the figure?

Note that they are asking for the angular momentum of the system, not just the pulley.

I don't think the 1/4 factor for the moment of inertia of the pulley is correct.

 

[postfan]

I attached the image. If so don't we need to know the distances between the blocks and the pulley?

 

[TSny]

You don't need those distances. Treat each block as a point particle located at the center of each block. Think about how to calculate the angular momentum of each block relative to the center of the pulley. You can use the definition of the angular momentum of a point particle relative to an origin.

 

[postfan]

The formula is mr^2, right, so you still need the distances?

 

[TSny]

The formula is mr^2, right, so you still need the distances?

That's not the formula for angular momentum. That's the moment of inertia of a single particle moving in a circle of radius r. The blocks are moving along straight lines. You should have covered the formula for the angular momentum of a point particle. It was probably at the very beginning of your study of angular momentum.

 

[postfan]

The 2 formula I know are m*r*v and I*w, we don't know both r and w, so how do we do it?

 

[TSny]

OK, the m*r*v formula can be used for a particle moving along a straight line with speed v. r is then the perpendicular distance from the origin to the straight line.

The speed v of one of the blocks is related to the angular speed of ω of the pulley. So in the formula m*r*v you can express v in terms of ω.

 

[postfan]

Ok so the formula is m*r*(w*r)=m*r^2*w, right?

 

[TSny]

Yes. That's it.

 

[postfan]

OK so the total angular momentum for the system is (M+m1+m2)*r^2*w, right?

 

[TSny]

OK so the total angular momentum for the system is (M+m1+m2)*r^2*w, right?

No, the part that deals with the pulley is not correct. You had the right approach for the pulley in your first post, but you didn't quite have the right expression for the moment of inertia, I.

 

[postfan]

Ok, so the angular momentum is M*r^2*w, right?

 

[TSny]

No, look at a table of moments of inertia.

 

[mshmsh_2100]

i met this problem once... but still cannot figure out the final formula of the angular momentum!

 

[mshmsh_2100]

i think the final formula for the angular momentum is (m1+m2)*v*R+M*omega*R^2, right?

 

[postfan]

OK, so according to the diagram the answer is .5*M*r^2*w, right?

 

[TSny]

OK, so according to the diagram the answer is .5*M*r^2*w, right?

Yes, for the pulley.

 

[postfan]

Do we need to add anything for the blocks?

 

[TSny]

Do we need to add anything for the blocks?

Yes. See post #9 for the angular momentum of each block.

 

[postfan]

OK, I got it. Thanks for your help!