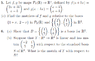Suppose you have two vectors \vec{x}, \vec{y} \in \mathbb{R}^2 such that \vec{y} = T(\vec{x}). Then you can write
\begin{align*}
\vec{x} = x_1 \hat{e}_1 + x_2\hat{e}_2 \\
\vec{y} = y_1 \hat{e}_1 + y_2\hat{e}_2
\end{align*}where \hat{e}_1=\begin{pmatrix}1 \\ 0 \end{pmatrix} and \hat{e}_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} are the standard basis vectors for \mathbb{R}^2. When you say T has the matrix \begin{pmatrix} -2 & 1 \\ 5 & 2 \end{pmatrix} with respect to this basis, it means that
\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix}-2 & 1 \\ 5 & 2 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}
In this problem, you're given a second basis, \hat{b}_1 = \begin{pmatrix} 1 \\ 5\end{pmatrix} and \hat{b}_2 = \begin{pmatrix} 1 \\ 6 \end{pmatrix}. As before, you can express \vec{x} and \vec{y} as a linear combination of them:
\begin{align*}
\vec{x} = c_1 \hat{b}_1 + c_2 \hat{b}_2 \\
\vec{y} = d_1 \hat{b}_1 + d_2 \hat{b}_2
\end{align*}Obviously c1 and c2 aren't going to be the same numbers as x1 and x2, and d1 and d2 won't be equal to y1 and y2. However, because \vec{y} = T(\vec{x}), c1, c2, d1, and d2 will be related by a matrix equation
\begin{pmatrix} d_1 \\ d_2 \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix}It is this matrix, \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, that you're looking for, the matrix of T relative to the basis B.
Now consider what happens when you choose c1=1 and c2=0. If you think about it a bit, you should be able to solve for the first column of the matrix. Conceptually, you're doing exactly the same thing you did in the previous problem.