barnflakes
- 156
- 4
Is my understanding correct:
Charge is conserved at a vertex. So the charges of particles pointing in towards a vertex and the charges of particles pointing out must be equal. Alternatively: The sum of the charges at a vertex must be zero.
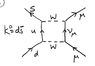
So if this is correct, can someone explain the attached diagram to me?
This is for the decay process:
\pi^- -> \mu^- + \overline{\nu_{\mu}}
To me, it should be a W^+ particle rather than W^-, since the charge at the first vertex is d = -1/3, anti-u = -2/3, and therefore if it's a W^- then the charge will be -2 rather than zero. If we put a W+ that solves the problem. Similarly on the other side, we have -1 from the muon and zero from the anti-muon-neutrino so we need a +1 from a W+ to conserve charge at the vertex.
Charge is conserved at a vertex. So the charges of particles pointing in towards a vertex and the charges of particles pointing out must be equal. Alternatively: The sum of the charges at a vertex must be zero.
So if this is correct, can someone explain the attached diagram to me?
This is for the decay process:
\pi^- -> \mu^- + \overline{\nu_{\mu}}
To me, it should be a W^+ particle rather than W^-, since the charge at the first vertex is d = -1/3, anti-u = -2/3, and therefore if it's a W^- then the charge will be -2 rather than zero. If we put a W+ that solves the problem. Similarly on the other side, we have -1 from the muon and zero from the anti-muon-neutrino so we need a +1 from a W+ to conserve charge at the vertex.