MaestroBach
- 53
- 4
- Homework Statement
- Find the frequency spectrum of the radiated power in spontaneous emission and use it to find the DOS.
- Relevant Equations
- Desired result below
All I'm reallly confused on this problem is what the expression for the emitted field is. As long as I've got that, I'm good to go, but I just don't know what to use. I've tried looking for an expression for the emitted field but I've had no luck. Would appreciate any ideas or someone telling me I'm missing something obvious.
(I'm told to find the Fourier transform of the field and go from there, which is why I'm trying to find the expression for the field)
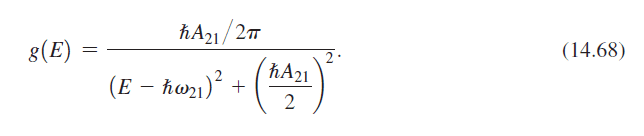
(I'm told to find the Fourier transform of the field and go from there, which is why I'm trying to find the expression for the field)