What is the Correct Minimum Force to Move a Ladder Against a Wall?

[bnoone]

Homework Statement

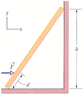
A uniform ladder is 10 m long and weighs 180 N. In the figure below, the ladder leans against a vertical, frictionless wall at height h = 8.0 m above the ground. A horizontal force is applied to the ladder at a distance 1.0 m from its base (measured along the ladder).

(a) If F = 50 N, what is the force of the ground on the ladder, in unit-vector notation?

(b) If F = 150 N, what is the force of the ground on the ladder, in unit-vector notation?

(c) Suppose the coefficient of static friction between the ladder and the ground is 0.38; for what minimum value of F will the base of the ladder just start to move toward the wall?

Homework Equations

∑\tau = r x F and ∑F = ma

The Attempt at a Solution

I got both parts (a) and (b) right so I don't need those.

For part (c), I summed the horizontal forces: ∑F_{x} = 0 = -F_{f} + F_{A} - N_{W}
where F_{A} is the applied force, F_{f} is the frictional force, and N_{W} is the normal force from the wall.

Then I summed the vertical forces: ∑F_{y} = 0 = N - W

Then I summed the torques using the base of the ladder as the axis of rotation: ∑\tau = 0 = Fsin(53) + 5(180)sin(37) - 10N_{W}sin(53)

Then I used N_{W} = μmg - F_{A} and substituted it into the torque equation and then plugged in all my numbers to solve for F.

I got F = 133 N, which is wrong and I'm not sure what I'm doing wrong.

 

[Chestermiller]

This equation NW = μmg - Ff is not consistent with your earlier relationship. It should read:
N_W = F_A-μmg

 

[bnoone]

Okay so after fixing that I have ∑\tau = 0 = F_{A}sin(53) +5(180)sin(37) - 10(F_{A} - (.38)(180))

Solving for F_{A}, I got 118.23 N which is still wrong. Did I make a mistake in summing the torques?

 

[haruspex]

There's no value in determining the angle. Just work with its trig ratios. These are handily rational here.

F_Asin(53) +5(180)sin(37) - 10(F_A - (.38)(180))

Think again about that 10.

 

[ehild]

Okay so after fixing that I have ∑\tau = 0 = F_{A}sin(53) +5(180)sin(37) - 10(F_{A} - (.38)(180))

Solving for F_{A}, I got 118.23 N which is still wrong. Did I make a mistake in summing the torques?

You left out sin(53) from the last term.
And better to use the ratios as haruspex said. Taking the angle 53° means a big rounding error.

ehild

 

[bnoone]

There's no value in determining the angle. Just work with its trig ratios. These are handily rational here.

Think again about that 10.

Should I use 6 (the horizontal distance from the base of the ladder to the wall) instead?

 

[ehild]

No. What is the leve[STRIKE]l[/STRIKE]r arm for N_W?

ehild

 

[haruspex]

No. What is the level arm for N_W?

ehild

"Level arm"? I'm unfamiliar with the term, so bnoone might be too.
bnoone, N_W acts horizontally. What is its distance from the point you're taking moments about?

 

[ehild]

"Level arm"? I'm unfamiliar with the term, so bnoone might be too.


http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html

ehild

 

[haruspex]

"Level arm"? I'm unfamiliar with the term, so bnoone might be too.


http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html

ehild

Oh, lever arm.

 

[ehild]

Yes, I mistyped it...

ehild

 

[bnoone]

"Level arm"? I'm unfamiliar with the term, so bnoone might be too.
bnoone, N_W acts horizontally. What is its distance from the point you're taking moments about?

Isn't it just the length of the ladder?

 

[haruspex]

Isn't it just the length of the ladder?

Torque = force * perpendicular distance. Is the ladder perpendicular to N_W?

 

[bnoone]

Torque = force * perpendicular distance. Is the ladder perpendicular to N_W?

Ohhh okay that makes sense. I forgot to include the sine of the angle between them. Thank you!