What is the Effect of Motion on the Velocity Vector of Light?

[bgq]

Hi,

Consider a source of light transmitting light at an angle θ with x-axis as seen in the following figure:

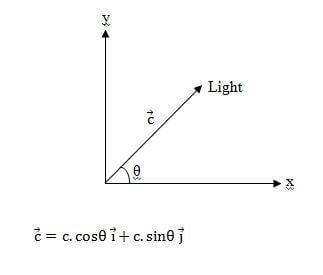
Now an observer looking at x-axis will determine the speed of light to be c.cos θ, and the one looking at y-axis determine c.sin θ.

How can we resolve this according to the principle of constancy of speed of light.

 

[Doc Al]

How can we resolve this according to the principle of constancy of speed of light.

What's to resolve? The speed of light is constant (invariant), but any component depends on what axis you choose. (And furthermore, the direction of a given light pulse is also frame dependent.)

 

[bgq]

Thanks Doc Al to your reply.

Consider an observer moving in the x direction with a speed c.cos θ.
According to this observer, there is no motion of the light along x-axis, so he will see the light moving parallel to y-axis with a speed c.sin θ ≠ c !

 

[Doc Al]

Consider an observer moving in the x direction with a speed c.cos θ.
According to this observer, there is no motion of the light along x-axis, so he will see the light moving parallel to y-axis with a speed c.sin θ ≠ c !

No, it doesn't work that way. What he'll see is the light moving with speed c in the y-direction.

You might want to look up the relativistic velocity transformations. They will show that different observers will see the light traveling in different directions, but always with speed c.

 

[bgq]

What confused me here is that time dilation and length contraction are not evident in the y direction because it is perpendicular to the motion. So the observer sees the light covers same distance during the same time along y-axis yielding v = c.sin (theta).

This is different to the case where the motion is along the propagation of light where time dilation and length contraction effects assure obtaining c for the speed of light.