ozon
- 8
- 1
Hello,
I am new at this forum. Firstly, I want to say I am happy to be a member of this forum. English is not my native language. So I can make some grammer and other mistakes. I try to write with no mistakes. If I make mistakes for writing, I apologize.
I have a question. You see a triangle in the picture. There are some vectors. h is height or short distance between p0 and V3. In the picture, you see an equation to find h. How do you prove this equation?
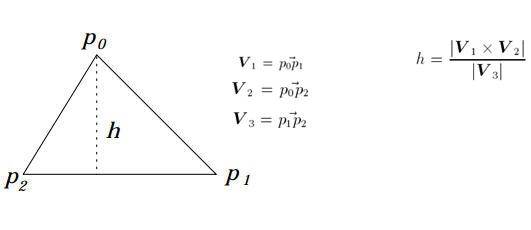
I am new at this forum. Firstly, I want to say I am happy to be a member of this forum. English is not my native language. So I can make some grammer and other mistakes. I try to write with no mistakes. If I make mistakes for writing, I apologize.
I have a question. You see a triangle in the picture. There are some vectors. h is height or short distance between p0 and V3. In the picture, you see an equation to find h. How do you prove this equation?