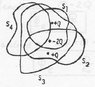
What is the flux though each of the surfaces

  • Thread starter Thread starter indigojoker
  • Start date Start date
  • Tags Tags
    Flux Surfaces
AI Thread Summary
The discussion centers on calculating the electric flux through four surfaces in relation to charge distribution. The initial calculations suggest a flux of -q/ε for surfaces 1 and 2, while surfaces 3 and 4 have a flux of 0. However, there is confusion regarding the specific question about the flux, as it depends on the positions of the charges and the definitions of the surfaces. Clarification on the context and configuration of the charges is necessary for accurate assessment. Understanding the electric field's influence on the flux is crucial for determining the correct values.
indigojoker
Messages
240
Reaction score
0
What is the flux though each of the surfaces:

I got:

Surface 1: -q/ε
Surface 2: -q/ε
Surface 3: 0
Surface 4: 0
 

Attachments

  • flux.jpg
    flux.jpg
    8.2 KB · Views: 413
Physics news on Phys.org
is this correct?
 
I have no idea what your question is! What flux are you talking about? The electric field due to those charges? That would depend on the precise position of the charges as well as the precise definitions of the 4 surfaces, which I cannot get from the picture.
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Flux through a cylindrical surface enclosing part of a sphere
Replies
9
Views
493
If closed integral of E.dS is zero over a surface, then...?
Replies
14
Views
852
Flux of constant magnetic field through lateral surface of cylinder
Replies
7
Views
2K
Is Electric Flux Through a Half Sphere Zero According to Gauss' Law?
Replies
20
Views
3K
Flux Through a Cube's Face with our Point Charge at a Corner
Replies
6
Views
4K
Electric Flux Through Spherical Surface Centered at Origin
Replies
3
Views
4K
Gauss' law problem -- Should the field due to both the inside and outside charges be taken into account?
Replies
28
Views
1K
Electric Field Inside a Gaussian Surface with Point Charge q
Replies
4
Views
2K
Flux linked with lower face of a cube
Replies
2
Views
1K
Earthing of two parallel conducting plates
Replies
11
Views
1K

Hot Threads

Recent Insights

Back
Top