What is the Initial Angular Acceleration of a Disk Released from Rest?

[klm]

A 5.0 kg, 60-cm-diameter disk rotates on an axle passing through one edge. The axle is parallel to the floor. The cylinder is held with the center of mass at the same height as the axle, then released.

What is the cylinder's initial angular acceleration?

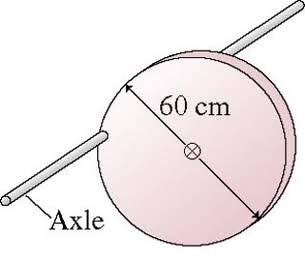
ok so this is what i think i should do:

Torque= I \alpha

and i need to find the F(weight)= mg = (5)(9.8) = 49 N
radius = .5(.6)= .3
Torque= Fd = 49(.3) = 14.7
14.7 = I \alpha
this is the part which i am not sure on, does I = .5 m r^2 = .5(5)(.3^2) = .225
14.7 .225 \alpha
\alpha = 65.33
but this answer is incorrect, and i do not know where i am making the mistake.

 

[klm]

please can someone help

 

[hage567]

Try using the Parallel Axis theorem to find the moment of inertia. This is needed because the axis of rotation is not through the centre of mass of the disk.

I = I_{CM} + MD^2

where I_{CM} is the moment of inertia for a solid disk, M is the mass of the disk and D is the distance from the centre of mass to the new axis.