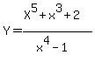What Is the Linear Oblique Asymptote of the Function (x^5+x^3+2)/(x^4-1)?

[Coco12]

Homework Statement

what is the linear oblique asymptote of (x^5+x^3+2)/(x^4-1)
?

Homework Equations

x-a/p(x) = q(x) +remainder

The Attempt at a Solution

I put in all the placeholders for the divisor and the numerator and got x as the equation for the linear oblique asymptote?? Is that right??

 

[Mentallic]

We would let

$$\frac{x^5+x^3+2}{x^4-1}\equiv \frac{(ax+b)(x^4-1)+p(x)}{x^4-1} = ax+b + \frac{p(x)}{x^4-1}$$

Where p(x) is a cubic polynomial or less (doesn't matter what it is exactly).If we expanded (ax+b)(x⁴-1) then we get

$$ax^5+bx^4-ax-b$$

But we ignore the -ax-b term because that will be a part of p(x) which we've already said we don't care about. So we want the constant a to be chosen such that $ax^5=x^5$ since the coefficient of $x^5$ on the LHS must be equal to the RHS, hence a=1, and b must be chosen such that $bx^4=0$ for the same reason, hence b=0.

But we ignore the -ax-b term because that will be a part of p(x) which we've already said we don't care about.

 

[Coco12]

Is the answer that I got correct? Thanks for taking the time to answer. I know how to do it just wondering if it's correct

 

[HallsofIvy]

Yes, y= x is the "liner oblique asymptote".

 

[Mark44]

Is the answer that I got correct? Thanks for taking the time to answer. I know how to do it just wondering if it's correct

No, this isn't correct. It's the equation of the rational function you started with.

To find the oblique asymptote, either do what Mentallic suggested or carry out the long division to get x + a proper rational function. In a proper rational function, the degree of the numerator is less than that of the denominator.

 

[Coco12]

Yes, y= x is the "liner oblique asymptote".

Ok thank you