jehan4141
- 90
- 0
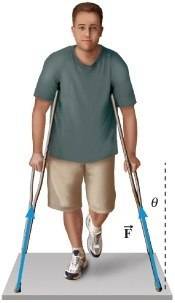
The person in the drawing is standing on crutches. Assume that the force exerted on each crutch by the ground is directed along the crutch, as the force vectors in the drawing indicate. If the coefficient of static friction between a crutch and the ground is 0.90, determine the largest angle θMAX that the crutch can have just before it begins to slip on the floor.
μ = 0.90
Ff = (Fn)μ
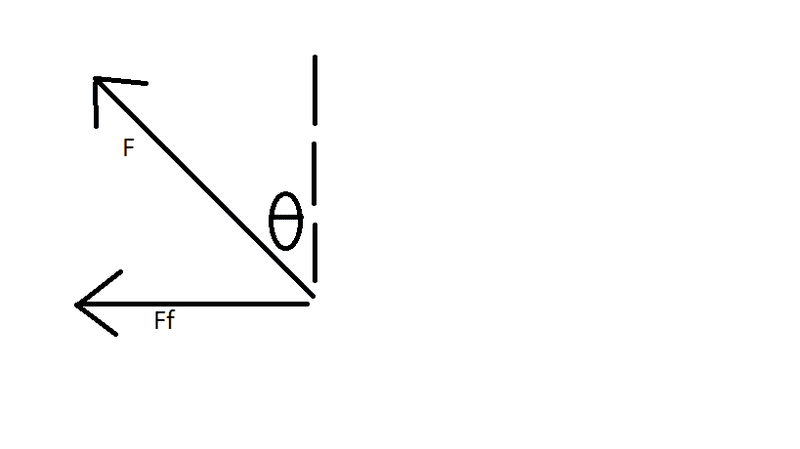
I know that I am missing a force for the problem to work, but I have thought about it for awhile and I can't seem to picture it. The normal force is supposed to be a force that is perpendicular to the surface...does that mean the normal force is Fcosθ? Is there supposed to be another force in the 4th quadrant? If yes, what is that force? Is it the force of the man pushing down on the crutch? If yes, does the force equal to F then?
μ = 0.90
Ff = (Fn)μ
I know that I am missing a force for the problem to work, but I have thought about it for awhile and I can't seem to picture it. The normal force is supposed to be a force that is perpendicular to the surface...does that mean the normal force is Fcosθ? Is there supposed to be another force in the 4th quadrant? If yes, what is that force? Is it the force of the man pushing down on the crutch? If yes, does the force equal to F then?