What is the maximum angle for a bob to slide upwards in a rotating funnel?

[stunner5000pt]

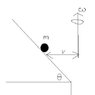
Ok have a look at the diagram below

A bob of mass m is on the inside of a funnel. The funnel is rotating with an angular velocity omega. The walls of the funnel has a friction coefficient of mu
The question is Show that there is an angle theta = theta max for which the bob cannot slide upwards if theta > theta max no matter how large the omega is. Determine theta max

So far here's what i have
force equation in the X direction (masses cancel out)

\omega^2 r cos \theta = \mu g cos \theta + \mu \omega^2 r sin \theta + g sin \theta

teh answer is \frac{1}{\mu} = tan \theta _{max}

seems to be derived by taking some limit as omega approaches a large number then the g sin theta nad the g cos theta part becomes negligbile. But i want to understand why this is being done. Any help would be greatly appreciated!

 

[stunner5000pt]

i think i got it by isolating for the theta and factoring out hte omega i get

Tan \theta = \frac{r - \frac{\mu g}{\omega^2}}{\mu r + \frac{g}{\omega^2}}
and now as omega reaches high value with respect to g and mu the pression approaches

tan \theta = \frac{r}{\mu r} = \frac{1}{\mu}

Since this is no longer dependant on omega for high values of omega the ball will definitely not slide upwards.

Also the mass will slide downwards if omega is sufficiently low because then omega must satisfy this condition

\omega^2 \geq \frac{g}{r} \frac{\mu cos \theta + sin \theta}{cos \theta - \mu sin \theta}

 

[gnome]

Nice move, dividing numerator & denominator by \omega^2 (wish I'd thought of it).

That's got to be it.