What Is the Maximum Horizontal Force Before the Penguin Slides Off the Sled?

[Nuha99]

Homework Statement

A sled weighing 60 N is pulled horizontally across snow so that the coefficient of kinetic friction between sled and snow is uk = 0.100. A penguin of 70 N rides on the sled. If the co. static friction between the penguin and the sled is us = 0.700 find the maximum horizontal force that can be exerted on the sled before the penguin begins to slide off.

Homework Equations

fs = us R, fk = uk R.

The Attempt at a Solution

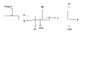
Please see the attached file for the force diagrams.

Forward force on the sled = F - fs - fk

In the absence of the static friction, penguin will slide backward with this force. But the penguin expereinces a force due to static friction fs.

F - fs - fk = fs

F = 2 fs + fk = 2 us R1 + uk R2 = 2 us m1g + uk (m1+m2)g = 111 N

Book answer is 104 N.

Can you check my force diagrams please?

Thanks.

 

[tiny-tim]

A sled weighing 60 N is pulled horizontally across snow so that the coefficient of kinetic friction between sled and snow is uk = 0.100. A penguin of 70 N rides on the sled. If the co. static friction between the penguin and the sled is us = 0.700 find the maximum horizontal force that can be exerted on the sled before the penguin begins to slide off.

Hi Nuha99!

I can't see your diagrams yet, but nor can I see anywhere in your equations where you've worked out the acceleration that the penguin can take.

Hint: start by applying Newton's second law to the penguin, and find that acceleration.

 

[Nuha99]

Attached file is not validated yet.

I did not find the acceleration of the sled. I found the net forward force on the sled. According to my understanding this net forward force is what will make the penguin to slide off.

Forward force on the sled = F - fs - fk

Note that fs is the static frictional force on penguin between penguin and the sled surface. By Newton's 3rd low, same but opposite force should act on the sled. This is the origin of fs in the above expression.

Now for the penguin to be stable, static frictional force = F - fs - fk

fs = F - fs - fk

Apparently some thing is not right. I solved this for F.
See my first post.

Thanks.

 

[tiny-tim]

I did not find the acceleration of the sled. I found the net forward force on the sled. According to my understanding this net forward force is what will make the penguin to slide off.

Hi Nuha99!

If there is acceleration (which there is),

then the force diagram must include accleration …

and so must the equations.

 

[Nuha99]

That does it. Thank you.