What is the maximum speed the rock can have before the string breaks?

[nahya]

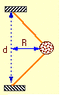
The rock is held by two of the same 40 cm strings with ends 70 cm apart and whirled in a circle between them. Neglect gravity.

--

i found the radius of the circular motion to be 19.36cm = 0.1936m.
now the question is "Now what is the maximum speed the rock can have before the string breaks?"

the hint says, "Find the angle between direction of acceleration and the string tensions. Use this to break the tensions into their components."

well... the direction of acceleration is towards the center...
i can get the the net x-force, which is x = 35cos(theta). i know the acceleration is towards the direction of x, but the magnitude is unknown, because the velocity is unknown, right?

or...
i thought of it this way.
both the strings can endure 35N of tension. they are in the opposite direction, so not 70N.
a = F/m = 35/0.57 =~61.40
v = sqrt(ar) =~ sqrt(61.40 * 0.1936) =~ 3.45.

that's incorrect, apparently.
i thought maybe the radius was the original radius, which is 56.40 (from sqrt(40^2 - 35^2)), but that is also incorrect...

i think the second way of thinking is correct, but maybe I'm not finding the right numbers to plug in.

 

[andrevdh]

Both tensions make the same angle (which can be determined from the geometry) with the horizontal. By resolving x- and y components one quickly comes to the conclusion that the tension in the upper string is the larger of the two. So one sets it to 35 N (the tensions in the strings are not the same). This leaves only one unknown - the tension in the lower string, which can therefore be solved (I assume the mass of the rock is given 0.57 kg?).

 

[nahya]

By resolving x- and y components one quickly comes to the conclusion that the tension in the upper string is the larger of the two.

why is that so?
wouldn't they have the same tension, as gravity is neglected?

 

[andrevdh]

Gravity neglected? The stone is not accelerating in the y-direction, so the y-component of the tension in the top string have to cancel the weight of the rock. The y-component of the tension in the bottom string adds to the weight of the rock, so the tension in the top string have to compensate for this too - in short the top string have to suppport the rock ,while the bottom string does not.

 

[nahya]

Gravity neglected? The stone is not accelerating in the y-direction, so the y-component of the tension in the top string have to cancel the weight of the rock. The y-component of the tension in the bottom string adds to the weight of the rock, so the tension in the top string have to compensate for this too - in short the top string have to suppport the rock ,while the bottom string does not.

why would i even need to worry about the weight?
since there's no gravitational attraction, weight can be ignored, right?

 

[Fermat]

Your problem says, "Neglect gravity", so gravity effects don't come into it. Imagine that you're doing this rotational motion somewhere out in outer space, without gravity effects.
In that case, the tension in both strings will be equal, with 35 N tension in each string.
The x-components of the string tensions will be what supply the centripetal force.
(I'm assuming that the x-direction is contained in the plane of motion)

Fc = 70cos@

and from the geometry, you can work out @.

Now use Newton's 2nd law to equate the centripetal force with the centripetal acceleration.