User1265
- 29
- 1
- Homework Statement
- 15. What is the minimum length of a plane mirror in order for you to see a full
view of yourself?
A 1/2 your height B 1/4 your height
C 3/4 your height D your full height
Q Why is answer of A given is the correct one,
- Relevant Equations
- angle of incidence = angle of reflection
15. What is the minimum length of a plane mirror in order for you to see a full
view of yourself?
A 1/2 your height B 1/4 your height
C 3/4 your height D your full height
Q Why is answer of A given is the correct one,
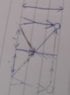
I understand pictorially how it is, since visually if you were to draw a mirror of the same length as the man, and draw the virtual image produced
you will see the reflected ray of light coming from the feet, emerge halfway up the mirror approximately en route to the real object (the man).
(Image explaining this is attached)
But is there not a more mathematical/geometrical way of explaining how A is so?
view of yourself?
A 1/2 your height B 1/4 your height
C 3/4 your height D your full height
Q Why is answer of A given is the correct one,
I understand pictorially how it is, since visually if you were to draw a mirror of the same length as the man, and draw the virtual image produced
you will see the reflected ray of light coming from the feet, emerge halfway up the mirror approximately en route to the real object (the man).
(Image explaining this is attached)
But is there not a more mathematical/geometrical way of explaining how A is so?