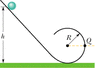What Is the Minimum Release Height for a Rolling Ball on a Loop-the-Loop Track?

[noname1]

In the figure below, a solid brass ball of mass m and radius r will roll without slipping along the loop-the-loop track when released from rest along the straight section. For the following answers use g for the acceleration due to gravity, and m, r, and R, as appropriate, where all quantities are in SI units.

(a) From what minimum height h above the bottom of the track must the marble be released to ensure that it does not leave the track at the top of the loop? (The radius of the loop-the-loop is R. Assume R r.)

(b) If the marble is released from height 6R above the bottom of the track, what is the magnitude of the horizontal component of the force acting on it at point Q?


Attempt

a)we know that total energy at the height h is potential energy when the body is at rest then
total energy at height h is mgh
Total energy at the bottom of the loop is (1/2)mu2
then mgh = (1/2)mu2
Now total energy the top of the loop is (1/2)mv2 +mg(2R)
Then mgh = (1/2)mv2 +mg(2R)
given that ball is on the verge of leaving the track when it reaches the top of the loop
then mg = mv2/R
then mgh = (1/2)(mgR) +mg(2R)
h = (R/2) + 2R
h = 5R/2


b) Now given that h = 6R
then total energy at height h is mgh
Total energy at the bottom of the loop is (1/2)mu2
then mgh = (1/2)mu2
then mg*6R = (1/2)mu2
Now total energy the point Q is (1/2)mv2 +mg(R)
Then (1/2)mu2 = (1/2)mv2 +mg(R)
mg*6R = (1/2)mv2 +mg(R)
Then 5mgR = (1/2)mv2
then 10mgR = mv2
Now total horizontal force on the ball at point Q is mv2/R = 10mgR/R = 10mg

But the system is saying my answers is wrong, what am i doing wrong?

 

[kuruman]

When you use energy conservation, you are not taking into account the rotational energy of the ball. You treat the ball as if it were sliding on a frictionless track. The problem clearly states that it rolls without slipping. The kinetic energy of the rolling ball should be

KE = (1/2)mu² (KE of the center of mass) + (1/2)Iω² (Rotational KE about the center of mass)

For rolling without slipping, u = ωr.