Saitama
- 4,244
- 93
Homework Statement
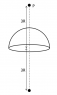
A thin hemispherical shell of mass M and radius R is placed as shown in figure. The magnitude of gravitational field at P due to the hemispherical shell is ##I_0##. The magnitude of gravitational field at Q due to thin hemispherical shell is given by
A)##I_0/2##
B)##I_0##
C)##\frac{2GM}{9R^2}-I_0##
D)##\frac{2GM}{9R^2}+I_0##
Homework Equations
The Attempt at a Solution
I tried the problem using spherical coordinates and ended up with some messy integrals. Since this is an exam problem, I wonder if I really need to solve those integrals as it would take a lot of time. (I solved the integrals using Wolfram Alpha and the result was not nice so I immediately dropped the approach.) I believe there is a shorter way to solve this.
Any help is appreciated. Thanks!