What Is the Nature of Orbits in an Inverse-Square Potential?

[stunner5000pt]

a particle of mass m moves in a potential V(r) = gamma/r^2 where the constant gamma >0

a) Sketch an effective potential and discuss the nature of the non zero angular momentum (L not zero) orbits without solving for the equation of the trajectory

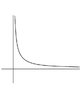
i know that V_{eff} = V(r) + \frac{L^2}{2mr^2}
here V_{eff} = \frac{1}{r^2} (\gamma + \frac{L^2}{2m})
so it will look like an inverse square graph as in teh digram


Calculate teh equation of the trajectories discuss their shapes and sketch a typical trajectory

one thing that's got me with this question is that i can't solve for r(t) or even r(phi) becuase their formulas involve using E which depends on (dr/dt)^2 and i don't end up getting anything solvable. Have a look
for r(t)
r(t) = \sqrt{\frac{2}{m} (E - V_{eff}(r))}
but E = \frac{1}{2} m \dot{r}^2 + V(r) + \frac{L^2}{2mr^2}
and that yeilds nothing useful
am i doing something wrong? Is energy supposed to be zero? But why?

there are two more parts which i will post later on. they are related to a and b.

 

[siddharth]

stunner,
Your answer to part A looks right. To find the equation of the trajectory, there is a nice trick you can apply. Make the substitution u=\frac{1}{r} and try finding u(\phi). You will see that the differential equation involving u and \phi can be solved and you will be able to find u(\phi).

In more detail, since r=\frac{1}{u}

\frac{dr}{dt} = -\frac{1}{u^2} \frac{du}{dt} = -\frac{1}{u^2} \frac{du}{d\theta} \frac{d\theta}{dt} where \frac{d\theta}{dt} = \omega.

So, substituting for v (\frac{dr}{dt}) in the energy equation you wrote in terms of \frac{du}{d\theta} and u, you get

E = V(u) + \frac{L^2 u^2}{2m} + \frac{1}{2}m(\frac{-L}{m}\frac{du}{d\theta})^2.

Now differentiate this equation with respect to theta. Can you see that \frac{du}{d\theta} will cancel?

The resulting differential equation you get can then be solved which will give you u (and hence r) as a function of theta. Can you take it from here?

 

[stunner5000pt]

Thank You !

alrighty so i had the right idea... the thing is we don't have a textbook for this course and there are so many versioins of the same ofrmula! Anyway here are the ther two questions

If (r_{m},\phi_{m}) are the planbe polar coordiantes of the perigee, evalute phi m (b) and from this calculate the impace parameter b in terms of the angle of scattering theta. Use this result to compute the differential scattering corss setion in terms of gamma, E and theta

The perigee represents a minimum distance between the mass and thecenter of motion. So to simply differentiate phi(r) w.r.t. r and plug that eqal to szero should yield the answer b.
if you could have a look at this thread too that would be awesome too
based on a similar concept
https://www.physicsforums.com/showthread.php?t=106913

 

[stunner5000pt]

stunner,
Your answer to part A looks right. To find the equation of the trajectory, there is a nice trick you can apply. Make the substitution u=\frac{1}{r} and try finding u(\phi). You will see that the differential equation involving u and \phi can be solved and you will be able to find u(\phi).

In more detail, since r=\frac{1}{u}

\frac{dr}{dt} = -\frac{1}{u^2} \frac{du}{dt} = -\frac{1}{u^2} \frac{du}{d\theta} \frac{d\theta}{dt} where \frac{d\theta}{dt} = \omega.

So, substituting for v (\frac{dr}{dt}) in the energy equation you wrote in terms of \frac{du}{d\theta} and u, you get

E = V(u) + \frac{L^2 u^2}{2m} + \frac{1}{2}m(\frac{-L}{m}\frac{du}{d\theta})^2.

Now differentiate this equation with respect to theta. Can you see that \frac{du}{d\theta} will cancel?

The resulting differential equation you get can then be solved which will give you u (and hence r) as a function of theta. Can you take it from here?

first of all I am not quite sure if i am supposd to be using that version of E in this problem
what does \frac{dE}{d \theta} yield that is useful?

also i get a differential equation with (u'')^2 which cnat be solved

 

[siddharth]

first of all I am not quite sure if i am supposd to be using that version of E in this problem
what does \frac{dE}{d \theta} yield that is useful?
also i get a differential equation with (u'')^2 which cnat be solved

In my post, \theta was the polar angle. So \frac{dE}{d \theta} is 0 because total energy is conserved. I'm pretty sure you don't get a (u'')^2 term. You could post and show where you are stuck.