What is the nature of the surface at the point of partial derivative equality?

In summary, the problem involves finding the point at which the partial derivatives of a given function are equal to zero and illustrating the surface of the function at this point. The solution involves finding the values for x and y that satisfy this condition and creating a contour plot to visualize the surface. The question is part of a difficult assignment, but the solution seems straightforward.
  • #1
KingBigness
96
0

Homework Statement



Let f(x,y)=1−x[itex]^{2}[/itex]−y[itex]^{2}[/itex]. Find the point at which

[itex]\frac{\partial f}{\partial x}[/itex] = [itex]\frac{\partial f}{\partial y}[/itex] = 0
and illustrate graphically the nature of the surface z = f (x, y) at this point.

The Attempt at a Solution



Just did the partial derivatives and got 2x=2y=0 hence x=0 and y=0

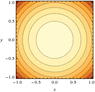
So illustrating z=f(x,y) at this point give z=1

Creating a contour plot I get the plot attached below.

This question is part of a difficult assignment I got from uni but this question seems way to easy in comparison to the rest of the assignment. I just want to make sure there isn't something I missed or is it really this simple?

Thank you
 

Attachments

  • MSP241419hb99bd9ig0gh4i00004aa457092c3a6ee2.gif
    MSP241419hb99bd9ig0gh4i00004aa457092c3a6ee2.gif
    8.7 KB · Views: 382
Last edited:
Physics news on Phys.org
  • #2
Any help?
 

FAQ: What is the nature of the surface at the point of partial derivative equality?

What is a partial derivative?

A partial derivative is a mathematical concept used to measure how a function changes with respect to one of its variables while holding all other variables constant. It is denoted by ∂f/∂x.

How is a partial derivative different from a regular derivative?

A regular derivative measures the rate of change of a function with respect to a single variable, while a partial derivative measures the rate of change with respect to one variable while holding all other variables constant.

What is the geometric interpretation of a partial derivative?

The geometric interpretation of a partial derivative is the slope of a tangent line to the graph of a function at a specific point, where the tangent line is parallel to one of the coordinate axes.

How are partial derivatives used in real-life applications?

Partial derivatives are used in many fields, including physics, economics, and engineering, to model and analyze complex systems and their behaviors. They can be used to optimize functions and make predictions in real-life scenarios.

Can a function have more than one partial derivative?

Yes, a function can have multiple partial derivatives, as it can have multiple independent variables. The number of partial derivatives will be equal to the number of independent variables in the function.

Similar threads

Partial Derivative Simplification
Replies
3
Views
1K
Discontinuous partial derivatives example
Replies
2
Views
333
Find f(x,y) given partial derivative and initial condition
Replies
6
Views
1K
Can anyone please verify/confirm these derivatives?
Replies
5
Views
1K
Determining domain for C^1 function
Replies
4
Views
756
Multivariable calculus proof involving the partial derivatives of an expression
Replies
4
Views
948
Calculating the partial derivative in polar coordinates
Replies
3
Views
2K
How to derive the associated Euler-Lagrange equation?
Replies
6
Views
1K
Multivariable calculus problem involving partial derivatives along a surface
Replies
9
Views
1K
Expanding Brackets with Partial Derivatives
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top