What is the net charge on the hollow conducting sphere?

[mitleid]

For the configuration shown in the figure below, suppose that a = 5.60 cm, b = 19.8 cm, and c = 27.9 cm. Furthermore, suppose that the electric field at a point 13.7 cm from the center is 3.44 x 10^3 N/C radially inward, while the electric field at a point 47.0 cm from the center is 1.03 x 10^2 N/C radially outward.

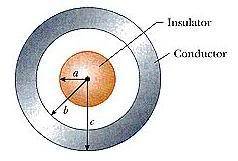
I've already answered half of this question, which is to find the charge on the insulating sphere as well as the surface charge on the inside of the hollow sphere (-7.18 x 10^-9 C and 7.18 x 10^-9 C respectively).

I'm having trouble with these :
find (b) the net charge on the hollow conducting sphere. and

(d) the total charge on the outer surfaces of the hollow conducting sphere.

What I did to try and get the net charge was basically the same as what I did for the insulating sphere...

(Field * R^2)/Ke = q

Any help is much appreciated! Pretty interesting problem...

 

[learningphysics]

Hint: First find the net charge within a gaussian sphere containing both the insulator and the hollow conductor...

Then subtract away the charge on the insulator to give the charge on the conductor... use the field at 47.0cm that they've given...

 

[mitleid]

yes!

I think I've got it now, thanks for connecting the dots for me... I'm actually a fairly visual learner, so until the picture makes sense in my mind it's difficult to realize the necessary calculations.

I should be doing well on the exam next week! Thanks again.

~Mitleid