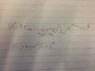What is the <r> for a hydrogen atom in n=2, l=1, m=0 state?

[Verruto]

Homework Statement

Hydrogen is in n=2, l=1, and m=0.
Wave function is ψ(r,θ,∅)=(1/4(√2pi)a_b^3/2)(r/a_b)(e^-r/2a_b)(cos(θ)

Find <r> for this state.

Homework Equations

P(r) = 4pir²|R(r)|²

<r> is equal to the integral from 0 to ∞ of P(r)dr

The Attempt at a Solution

I understand that you need to go from the wave function to R(r) and then P(r) to put that in the <r> equation. I am just not sure how you do the first step.
I put the equations in the picture below to better visualize it. Thanks in advance!

 

[DrClaude]

The equation for $P(r)$ already takes into account the fact that you have integrated the spherical harmonic over $\theta, \phi$, and this is where the factor $4 \pi$ comes from. So you would have to remove the angular part from the initial wave function.

That said, I believe that you will learn more if you don't take that ready-made equation, but calculate it from first principles:
$$
\langle r \rangle = \int_{0}^{2 \pi} \int_{0}^{\pi} \int_{0}^{\infty} \psi^* r \psi r^2 dr \sin \theta d\theta d\phi
$$

Note that you have a factor $r$ missing in your description of the integration step, it should be
$$
\langle r \rangle = \int_{0}^{\infty} P(r) r^3 dr
$$