RedBarchetta
- 49
- 1
[SOLVED] Work: Spherical Problem
A tank is full of water. Find the work W required to pump the water out of the spout. (Use 9.8 for g and 3.14 for [PLAIN]http://www.webassign.net/images/pi.gif.[/URL] Round your answer to three significant digits.) W=_________
r=3
h=1
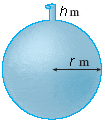
To set up this problem, I started by taking the area of one slice of water to be pi r^{2} multiplied by an infitesimally small height \Delta y to get volume. Then multiply this by the density of water; 1000 kg/m^{3} to get the volume of one slice.
Now I want R as a function of, let's say y. We know the area of a circle is r^{2}2+y^{2}=3^{2}. So r=sqrt(9-y^{2}). Also, the distance for any slice from the top is 7-y.
After this I tried integrating from zero to six of the function 1000*pi*(9-y^{2})*(7-y)*y. This came out to be negative...in fact -36000*pi..
Apparently, that is wrong. Where did I go wrong?
Thanks.
Homework Statement
A tank is full of water. Find the work W required to pump the water out of the spout. (Use 9.8 for g and 3.14 for [PLAIN]http://www.webassign.net/images/pi.gif.[/URL] Round your answer to three significant digits.) W=_________
r=3
h=1
The Attempt at a Solution
To set up this problem, I started by taking the area of one slice of water to be pi r^{2} multiplied by an infitesimally small height \Delta y to get volume. Then multiply this by the density of water; 1000 kg/m^{3} to get the volume of one slice.
Now I want R as a function of, let's say y. We know the area of a circle is r^{2}2+y^{2}=3^{2}. So r=sqrt(9-y^{2}). Also, the distance for any slice from the top is 7-y.
After this I tried integrating from zero to six of the function 1000*pi*(9-y^{2})*(7-y)*y. This came out to be negative...in fact -36000*pi..
Apparently, that is wrong. Where did I go wrong?
Thanks.
Last edited by a moderator: