How do you calculate the work required to pump water out of a hemisphere tank?

[ju456one]

<Moderator's note: Moved from a technical forum and thus no template.>

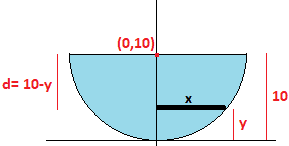
> The tank (hemisphere) is full of water. Using the fact that the weight of water is 62.4 lb/ft3, find the work required to pump the water out of the outlet. The radius of the hemisphere is 10.

$V =\pi x^2 h$

using the equation of a sphere with a center in $\ (0,10)$

$\ x^2 + (y-10)^2 = 100$

$\ x^2 = 20y-y^2$

And the volume is:

$V =\pi (20y-y^2) \Delta y$

the force would be:

$F =62.4 \pi (20y-y^2) \Delta y$

And the distance as the image says is:

$d = (10-y)$

Finally the work would be:

$\int_0^{10} 62.4 \pi (20y-y^2) (10-y)\, dy$

And the answer gives me $156000 \pi$ but according to my textbook the answer have to be $41600\pi$

what I'm doing wrong?

 

[LCKurtz]

I set it up a different way and got the same answer as you.