What is the Speed of the Lowest Bead as the Upper Bead Passes Over the Peg?

[omc1]

Homework Statement

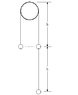
A massless string having three beads of identical mass attached to it is placed so that it hangs at rest on a thin frictionless peg, as shown. Of course, the string then slides over the peg and falls to the ground. If h = 55 cm, what is the speed of the lowest bead at the instant when the upper bead passes over the peg

Homework Equations

ke=1/2mv^2 w=fd

The Attempt at a Solution

Δke=fd 1/2mv^2 final =0 1/2mv^2 (initial)=fd
d=55cm i got 3.28m/s but that's not right

 

[gneill]

A diagram or at least a better description of the setup would be helpful.

 

[omc1]

three beads are on a string and and laying over a peg protruding from the wall...so that beads one and two are even (bead one hangs on the left of peg and bead two on the right) and the third bead hangs down on right just farther down. h = the distance from the peg to the first (or second bead) and also the distance from first bead to third bead so H =2h...

 

[gneill]

So, something like this?

Can you provide a bit more detail about the calculation you performed? What was your reasoning?

 

[omc1]

yes!

 

[omc1]

i figured if i found the speed of the first bead going over the peg it would be the same as the thrid bead. so i made the first bead start at 0 and end at 55 cm so i did 1/2mv^2=mgd and got 3.28m/s

 

[gneill]

i figured if i found the speed of the first bead going over the peg it would be the same as the thrid bead. so i made the first bead start at 0 and end at 55 cm so i did 1/2mv^2=mgd and got 3.28m/s

Okay, but you do realize that a bead cannot spontaneously gain energy by falling upwards, right? Only something falling in the gravitational potential can gain kinetic energy, while something rising against gravity will lose it.

So, identify the source of the energy gain and offset it against any losses...

 

[omc1]

the total distence and the total mass of 2 and 3 beads are what's giving bead one the potential to move upward so pe=m(sub total)g2h ??

 

[gneill]

Be sure to account for ALL the changes in PE.

 

[omc1]

well wouldn't the final pe just be zero bc it hits the ground??

 

[gneill]

well wouldn't the final pe just be zero bc it hits the ground??

There is no mention of the ground anywhere in the problem statement.

Some beads rise, some beads fall... what's the total change in PE?

 

[omc1]

pe=mgh(final)-mgh(initial) so if bead one starts out at zero and ends at 55cm then pe=mgh(final)...

 

[gneill]

As I said, some parts are rising and some parts are falling. The parts that are rising are going to to gain PE. The ones that are falling are going to lose PE. Do the sums!

 

[omc1]

ok but i don't see where ur going with this...iam just confused n suck at physics

 

[gneill]

ok but i don't see where ur going with this...iam just confused n suck at physics

It takes energy to raise a mass in a gravitational field. You also get energy out if you lower a mass in a gravitational field. Energy is conserved. So if some of the mass is rising and some of the mass is falling, what's the net change in energy that results from all the movements? You can't just look at the change in height of one bead. You must take ALL of them and their motions into account.

 

[omc1]

so the total energy for the system would be the sum of pe and ke ...?

 

[gneill]

so the total energy for the system would be the sum of pe and ke ...?

Yes, and the sum is a constant (conservation of energy). But you get to choose your zero reference points for convenience. The system starts with zero KE (no motion). You could also assign a zero PE reference individually to the masses at their initial locations and just sum their changes in PE for a total change in PE.

 

[omc1]

ok i seee now thanks so much!

 

[gneill]

ok i seee now thanks so much!

Glad to help!