What is the thread's length pulled and the variation factor of velocity?

[Icaro Amorim]

Homework Statement

Hello, guys. I'm not a native english speaker, so don't mind if I wrote something incorrectly (if you find any error or difficulty in what I wrote just inform me, please).

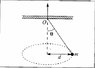
A little ball is hold by a thread of negligible mass which moves round a vertical axis with constant velocity. It keeps a distance of 0,5m from the axis when the anglo θ is equal 30º (as shown in the figure uploaded). The thread goes through a little hole O in a slab and it is slowly pulled up until the angle Θ becomes 60º. What is the thread's length pulled? What is the variation factor of velocity?

Homework Equations

L = rxmv, T*senΘ=mv²/R and T*cosΘ-mg = 0

The Attempt at a Solution

I've tried solving this question this way:
"let T₁ be the tension when θ₁=30º, m*g be the weight and v₁ be the velocity. Then we can get tg30º = (m*(v₁)²/R₁)/(mg) = √3/3 => √3/3*g=v²₁/R₁ (I)
and when Θ=60º we have √3g=v²₂/R₂. (II)
From these equations I divided I by II:
1/3= (v₁/v₂)²*R₂/R₁ and obtained (III). But we threen unknows (v₂, R₂, v₁) and only one equation.

I imagine the angular momentum might conserve in the perpendicular direction to the plane of motion of the mass once it is slowly pulled up, but I have no idea how to apply this.

P.S.: I used R but it is the same in meaning as d in the figure.

 

[voko]

You have two equations, (I) and (II). Add to them conservation of angular momentum, and you will have three equations and three unknowns. Solve.

 

[Icaro Amorim]

That's the problem. I don't know how to apply conservation of angular momentum. I tried M*v1*(R1/tgθ1) = M*v2*(R2/tgθ2) where R/tgθ is the distance from the point O to the plane of motion and it was incorrect. Can you tell me why?

 

[voko]

You said that $R$ was the same as $d$ in the figure. Then angular momentum is simply $m v_1 R_1$ and $m v_2 R_2$.

 

[HalfLostAndSearching]

Hello, great job in attempting to solve this problem. You are correct in thinking that angular momentum is conserved in this system. In fact, angular momentum conservation is a fundamental principle in physics that states that the total angular momentum of a system remains constant unless acted upon by an external torque.

In this case, the system consists of the ball, the thread, and the slab. Initially, the ball is moving in a circular motion with a constant velocity and the thread is at an angle of 30º. When the thread is pulled up, the angle changes to 60º, but the ball continues to move in a circular motion. This means that the angular momentum of the ball remains constant.

Using the equation L = rxmv, where r is the distance from the axis, m is the mass, v is the velocity, and x is the distance from the axis to the center of mass, we can see that the angular momentum is directly proportional to the velocity. This means that as the thread is pulled up, the velocity of the ball must increase in order to keep the angular momentum constant.

To solve for the length of the thread pulled, we can use the equation for centripetal force, T = mv²/R, where T is the tension in the thread, m is the mass, v is the velocity, and R is the radius of the circular motion. We know that the tension in the thread remains constant, so we can set the equations for tension at the two different angles equal to each other and solve for the velocity at each angle. This will give us two equations with two unknowns (v1 and v2).

Once we have the velocities, we can use the equation for angular momentum to solve for the length of the thread pulled. We know that the angular momentum remains constant, so we can set the equations at the two different angles equal to each other and solve for the length of the thread pulled.

As for the variation factor of velocity, we can use the equation v2/v1 = √(R1/R2), where v1 is the initial velocity, v2 is the final velocity, R1 is the initial radius, and R2 is the final radius. This will give us the ratio of the two velocities, which can then be used to find the variation factor.

I hope this helps and good luck with your homework!