Master1022
- 590
- 116
- Homework Statement
- We are using the following gear in the reverse gear mode (brake applied to the cage shaft and engine is driving the ring gear) and are traveling at 1 m/s. The wheel radius is 0.2 m. What is the torque that the engine needs to provide 2kW of power? Also, what is the torque in the wheels?
- Relevant Equations
- ## v = \omega r ##
Hi,
I was just working through this gearbox problem and the answer key has different results to mine. I thought that I should show my working to see where the error is on their part or mine?
This is the gear box (for reference, ## N_s = 32 ##, ## N_p = 16 ##, and ## N_r = 64 ##)
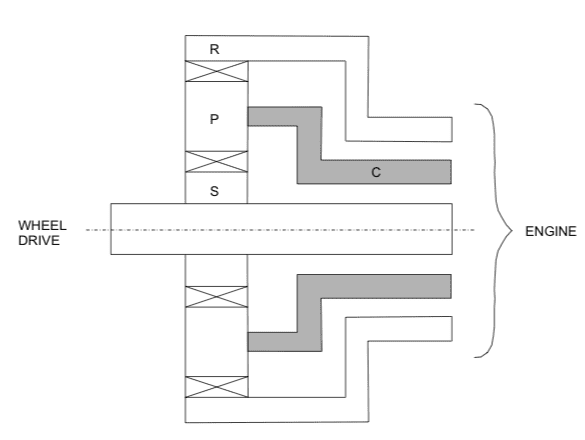
My attempt:
For the reverse gear operation (brake applied to the cage shaft and engine is driving the ring gear), I found that the ratio of:
$$ \frac{\omega_{out}}{\omega_{in}} = \frac{\omega_s}{\omega_r} = -2 $$
Therefore, ## v = \omega_{s} r =1 ## which yields ## \omega_s = 5 ## rad/s. Therefore, we get ## \omega_r = -2.5 ## rad/s. We also assume that the gear train is 100% efficient and therefore:
$$ P_{s} = 2000 = T_s \omega_s \Rightarrow T_s = 400 Nm $$
Once again, by using power conservation:
$$ T_r \omega_r = T_s \omega_s \Rightarrow T_r = T_s \frac{\omega_s}{\omega_r} = -2T_s = (-) 800 Nm $$
The answer has the same answer for the torque of the wheels, but then has ## |T_r| = 200 Nm ##. Have they just flipped the fraction the wrong way round or have I made the error. I keep trying to rework through the problem and I am getting the same answer (800)...
Also, just one more follow up question. Given that the gearbox is in equilibrium (I think this is an assumption we make), would I do the following if we were asked to find the torque provided by the brake?
$$ T_{brake} + T_r + T_s = 0 \Rightarrow T_{brake} = 800 - 200 = 600 Nm $$
Thank you. Any help is greatly appreciated
I was just working through this gearbox problem and the answer key has different results to mine. I thought that I should show my working to see where the error is on their part or mine?
This is the gear box (for reference, ## N_s = 32 ##, ## N_p = 16 ##, and ## N_r = 64 ##)
My attempt:
For the reverse gear operation (brake applied to the cage shaft and engine is driving the ring gear), I found that the ratio of:
$$ \frac{\omega_{out}}{\omega_{in}} = \frac{\omega_s}{\omega_r} = -2 $$
Therefore, ## v = \omega_{s} r =1 ## which yields ## \omega_s = 5 ## rad/s. Therefore, we get ## \omega_r = -2.5 ## rad/s. We also assume that the gear train is 100% efficient and therefore:
$$ P_{s} = 2000 = T_s \omega_s \Rightarrow T_s = 400 Nm $$
Once again, by using power conservation:
$$ T_r \omega_r = T_s \omega_s \Rightarrow T_r = T_s \frac{\omega_s}{\omega_r} = -2T_s = (-) 800 Nm $$
The answer has the same answer for the torque of the wheels, but then has ## |T_r| = 200 Nm ##. Have they just flipped the fraction the wrong way round or have I made the error. I keep trying to rework through the problem and I am getting the same answer (800)...
Also, just one more follow up question. Given that the gearbox is in equilibrium (I think this is an assumption we make), would I do the following if we were asked to find the torque provided by the brake?
$$ T_{brake} + T_r + T_s = 0 \Rightarrow T_{brake} = 800 - 200 = 600 Nm $$
Thank you. Any help is greatly appreciated

