What is the Velocity of Point P relative to Point O in a Linkage Arm System?

[Dusty912]

Homework Statement

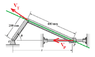
I uploaded the picture to this problem, but it asks what the relative velocity of point p is to point o when theta is equal to one and the derivative of theta in respect to time is also positive 1. the picture explains everything.

Homework Equations

Tangential velocity is equal to omega (angular velocity) times the radius. the radius would be the 200 mm arm in this case.

The Attempt at a Solution

Honestly, my solution seems too simple, but the logic seems right to me. I basically just used the equation
V_t=ω*r
the V_t=200*1=200

then just used the cosΘ=V_xt/V_t

and solved for V_xt with Θ=1 rad and V_t = 200

the answer I got was 108.0598mm/s

I went off the idea that the V_tx value would always have to be equal to the velocity of PI may have gone horribly wrong somewhere but I'm not really sure if I have. Thanks for the help, you guys and girls rock!

 

[andrevdh]

I don't think your assumption is correct.
The motion of P would only be the same if the x distance between the two point were fixed, which it is not, it changes as the connection point moves up or down.

 

[TomHart]

This is a tricky little problem that I spent quite a bit of time thinking about.

I went off the idea that the Vtx value would always have to be equal to the velocity of P

Yeah, I am in agreement with andrevdh that your assumption is not correct. Here's why I think that. Start by disconnecting the two rods at the connection point (I am going to call that point T for Top) and taking the shorter rod completely out of the picture. Then if you pull vertically upward at point T on the remaining rod (the right-hand rod), that will produce movement of point P to the left. Note that leftward velocity of point P can be produced by vertical velocity (only) of point T. For that reason, your assumption is incorrect that the velocity of point P is equal to the x component of the velocity of point T. The only times when the velocity of P is equal to the horizontal velocity of point T is when the left rod is vertical (θ = 90°) - the point when the vertical component of the velocity of point T is equal to 0, or when the left rod is horizontal (θ = 0°) - the point when the horizontal component of the velocity of point T is equal to 0. Edit: I reversed θ = 0° and θ = 90° above; I had them backwards.

The way I see it, the velocity of point P in the x direction is the sum of two components:
1) the velocity of point P due to the x component of the velocity of point T (these two are equal)
2) the velocity of point P due to the y component of the velocity of point T (the relative size being dependent on the angle θ)

So I agree that your answer of 108.0598 mm/s is the x component of the velocity of point T. Now you have to find the velocity of point P produced by the vertical component of the velocity of point T.

Please post when you come up with a final answer so we can compare results. Thank you.

 

[Dusty912]

sp would I just have to include the vertical component of the tangential velocity as well? not really sure where to go from here

 

[TomHart]

sp would I just have to include the vertical component of the tangential velocity as well? not really sure where to go from here

You can't just include the vertical component of the tangential velocity; you have to calculate the horizontal velocity of point P due to the vertical velocity of [what I call] point T.
Once again, imagine that the left rod has been removed and that the right rod is lying horizontally. If you grab ahold of point T and start to pull it vertically upward with constant velocity, point P will start moving very slowly, at first, toward the left. But the higher point T gets, the greater the velocity that point P will move toward the left. The ratio of those two velocities (point T's upward velocity relative to point P's leftward velocity) changes as the angle θ changes.

 

[Nidum]

Clue 1 : This is in the problem statement . Why do they quote the angular velocity in differential form ?

Clue 2 : Write down a simple geometric function relating angle of crank to axial position of crosshead .

 

[TomHart]

Clue 1 : This is in the problem statement . Why do they quote the angular velocity in differential form ?

Clue 2 : Write down a simple geometric function relating angle of crank to axial position of crosshead .

Thank you for your comment. I think this method is more straightforward than what I was suggesting - once one can actually come up with that geometric function. Just to clarify due to my lack of understanding of the terms, "axial position of crosshead" is basically point P's position along the x axis. Is that correct? Thank you.

 

[Nidum]

Just to clarify due to my lack of understanding of the terms, "axial position of crosshead" is basically point P's position along the x axis. Is that correct?

Yes - that's it .

 

[Dusty912]

well the law of cosines relates all of those

 

[Nidum]

once one can actually come up with that geometric function

Use a construction line dropping vertically from crank pin to horizontal axis .

 

[Dusty912]

so then tanΘ=(opposite)/200mm

 

[Dusty912]

sorry not tangent

 

[Dusty912]

I meant sine or cosine relations could be used

 

[Dusty912]

such as sinΘ=(opposite)/200mm or cosΘ=(adjacent)/200mm

 

[TomHart]

such as sinΘ=(opposite)/200mm or cosΘ=(adjacent)/200mm

Yes, keep going. I am going to take a back seat on this one and defer to Nidum.

 

[Dusty912]

hmm could you just let me know if this next step is right? So this would be my position function. by taking the derivative with respect to time, I would get my velocity function?

 

[Nidum]

by taking the derivative with respect to time, I would get my velocity function?

Yes- that's it .

But you haven't got the geometric function yet .

 

[Dusty912]

ok but wouldn't the derivative of say the cosine function be -sinΘ=0 (my velocity function)

 

[Nidum]

Don't quite understand what you are saying there ?

 

[Dusty912]

well I said earlier that cosΘ=(adjacent)/200mm would be my position function. and that it's derivative with respect to time would be my velocity function? I guess I made a mistake in my derivation. But how should I approach this derivation?

 

[Dusty912]

or would it be better to state the function as cosΘ=x/r where r is the radius which is 200 mm? and then I would take the derivative with respect to x?

 

[Dusty912]

and would I be using the combination of the derivatives of both the sine and cosine functions to find my final answer? or just one of them? (that is the commination of the vertical and horizontal components of velocity)

 

[Nidum]

It's past midnight now in UK so I'm for bed . Back tomorrow am .

Maybe TomHart or someone else can help you finish this problem in the meantime ?

 

[Dusty912]

should I message him?

 

[Dusty912]

Can anyone else help me with this? Nidam lives in the UK and has gone to bed.

 

[TSny]

Using the law of cosines to determine s in terms of θ and then using that to find V_p should work. But it's somewhat tedious.

You might consider a different approach. Consider the diagram below. The green line is a reference line drawn along the 400 mm rod.

The 400 mm rod cannot change its length. So, what does this constraint tell you about the projections of V_T and V_p along the green line?

 

[haruspex]

Can anyone else help me with this? Nidam lives in the UK and has gone to bed.

The key is to consider velocities along the line of the arm connected to P.
Call the joint at the top Q. What can you say about the instantaneous relative motions of P and Q in the PQ direction?

TSny beat me to it... with a diagram too!

 

[TSny]

TSny beat me to it... with a diagram too!

My lucky night (It's hard to beat haruspex to the punch.)

 

[Dusty912]

Using the law of cosines to determine s in terms of θ and then using that to find V_p should work. But it's somewhat tedious.

You might consider a different approach. Consider the diagram below. The green line is a reference line drawn along the 400 mm rod.
View attachment 128561

The 400 mm rod cannot change its length. So, what does this constraint tell you about the projections of V_T and V_p along the green line?

It's saying that THE PROJECTIONS of V_p and V_t are changing at the same rate

 

[Dusty912]

sorry if I seem pretty lost on this, I just really want to get this one down since I've been working on it for so long

 

[haruspex]

It's saying that THE PROJECTIONS of V_p and V_t are changing at the same rate

Vp and Vt are velocities. There is a simpler relationship than just that they change at the same rate.

 

[Dusty912]

they are equal to each other

 

[Dusty912]

well actually that doesn't really make any sense, since V_t is a constant velocity and V_p is not

 

[Dusty912]

is it just that the projections are always equal to each other?

 

[haruspex]

well actually that doesn't really make any sense, since V_t is a constant velocity and V_p is not

The constancy does not matter since we are only concerned with instantaneous velocities at the given position. Anyway, even if |Vt| is constant the vector Vt is not..

is it just that the projections are always equal to each other?

Yes. Do you see why?

 

[Dusty912]

yes I see why. because the vector is dependent upon magnitude and direction

 

[Dusty912]

ok so the horizontal components are always equal to each other. but don't the vertical compontents of the tangential velocity also effect the horizontal velocity at P?

 

[haruspex]

ok so the horizontal components are always equal to each other.

No, as you wrote earlier:

the projections are always equal to each other?

.. but projections in which direction? What direction did I say to consider?

because the vector is dependent upon magnitude and direction

No. What physically constrains the relative motions of P and Q?

 

[Dusty912]

the projections in the horizontal direction are the ones we are considering?

the 400mm are physically constrains these two

 

[haruspex]

the projections in the horizontal direction are the ones we are considering?

No.

the 400mm are physically constrains these two

Right. So what does that mean for their relative motion in the PQ direction?
You might find it easier to think about in the frame of reference of P. Relative to P, can Q get any closer or further away? What does that say about the direction of the relative velocity of Q?

 

[Dusty912]

no Q cannot get any closer to P, the velocities would be in the same direction for P and Q

 

[Dusty912]

ok so I attempted the problem again with the information you gave me. I basically found the angle between V_t and the action line. which was 32.415 degrees. Then I found V_t by multiplying the radius by the angular velocity (200mm/s) the I used cos(32.415)*200mm/s to find my answer. so basically I used the graphic that the other member had drawn for me. and projected V_t onto the line PQ

 

[Dusty912]

so the velocity of P should match the velocity of V_t onto the line PQ. my logic was because when the rotating arm is at 0 radian, The velocity at P is zero, and so is the velocity of V_t projected onto the line.

 

[haruspex]

so the velocity of P should match the velocity of Vt onto the line PQ.

The components of the velocities in the PQ direction should be the same, yes. What answer does that give you?

when the rotating arm is at 0 radian, The velocity at P is zero, and so is the velocity of Vt projected onto the line.

Yes, and that fits with the general relationship described above. Because PQ is a constant distance, the relative velcities of P and Q must always be the same in the PQ direction.

 

[Dusty912]

the answer I got was 168.84 mm/s

 

[Dusty912]

and is the max speed of P, the tangential speed of the arm (200mm/s)? it couldn't go faster than that right? just curious about that

 

[TomHart]

I got an answer greater than 200 mm/s for this problem: However, I have very low confidence in my result. Is there anyone else who has worked this problem through and can comment on Dusty's result of 168.84 mm/s - whether it is correct or not?

Edit: By the way, I stumbled in trying to find a relationship between the angle θ and the position of point P - using law of cosines or any other method - along the x axis. I was not able to do it.

 

[gneill]

I got an answer greater than 200 mm/s for this problem: However, I have very low confidence in my result. Is there anyone else who has worked this problem through and can comment on Dusty's result of 168.84 mm/s - whether it is correct or not?

Edit: By the way, I stumbled in trying to find a relationship between the angle θ and the position of point P - using law of cosines or any other method - along the x axis. I was not able to do it.

I also find a value greater than 200 mm/s.

If you use the law of cosines then you'll have to solve a quadratic and choose the correct root. Another approach is to break the geometry into a pair of triangles and use a mix of trig and Pythagoras. Both methods yield the same expression for the length OP in terms of θ.

 

[Dusty912]

I am going to try it with law of cosines. it looks like it will make more sense that way.