Sneakatone said:
No. Well, it is like this:
You see, consider the situation when you are measuring a quantity, say
x, which is the position vector of a particle. When you saw it at time t, It's position was
x. Then you saw it after a time t + dt(note that d is not a coefficient or a constant as I had said earlier). The position had become
x+dx. So, now the rate of change of
x with respect to time is
\frac{(x+dx)-x}{(t+dt)-t} which is \frac{dx}{dt} which is also called velocity
I'm sure you knew the above stuff but it never hurts to go back to the basics.
Now take the case of k
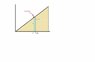
x. To make some sense, let's assume the particle moving up an inclined plane, which starts with 0 height at the origin and becomes taller as you move to the such that its height x units away form the origin is kx.( picturize this in your mind or see my attachment for the diagram). Right, now your objective is to find the vertical component of velocity.
Now, say at time t you saw the body at the X coordinate
x. So its Y coordinate would be kx according to our earlier assumption.
At time t+dt, you see that its x coordinate is x+dx ok? So then its Y coordinate would be k(x+dx) right?
Now you define the vertical component of velocity as rate of change of Y coordinate with time.
And also differentiating y w.r.t. time.
So this would be \frac{k(x+dx)-kx}{(t+dt)-t}
that is k\frac{dx}{dt} (note that dx and dt don't cancel each other)
Followed me so far? Now we come to the real business: The position vector of center of mass of your system (of total mass M and m
1, m
2 ...etc. are masses of the particles in the system) is defined as
X_{CM}=\frac{m_1x_1 +m_2x_2 +...}{M}
this can also be written as X_{CM}=\frac{m_1x_1}{M} + \frac{m_2x_2}{M} ...
Now the velocity of the center of mass is defined as rate of change of X
CM with time.
So using the argument that I have previously used in my height example,as each of those \frac{m_i}{M}x_1 (because \frac{m_i}{M} is a constant like k) change with respect to time as \frac{m_i}{M}\frac{dx_i}{dt} okay?
So \frac{dX_{CM}}{dt}= \Sigma \frac{m_i}{M}\frac{dx_i}{dt}
This means that the velocity of the center of mass is the same as the sum of the products of the particle products and velocities divided by the total mass.
Just for an exercise to help you understand better, try getting the relation between the acceleration of the center of mass and the individual accelerations of the systems particles.