What is the voltage on capacitance C2 immediately after commutation in circuits?

[Ivan Antunovic]

Homework Statement

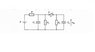
By the time t = 0, the network was in steady state. At time t = 0, the switch is turned on. Find the voltage on the capacitance C2 immediately after the commutation.[/B]

Homework Equations

KCL i(-0) = -ic1(+0) - ic2(+0)
KVL E-i(-0) * R-Vc1(-0) = 0
Vc1(+0) = Vc2(+0)

The Attempt at a Solution

The picture attached,
The current at t = - 0 is i(-0) = E/R+R1, at time t = +0 ,R1 and R2 are both being short circuited by C2,but are my KVL and KCL equations even right?I think I messed up with times +0 and -0.

How do I approach commutation in circuits?
It's really confusing for me since I've just started learning about it.

 

[gneill]

Your voltage across C1 for time t=0- is fine. It's the result of the R&R1 voltage divider.

For the instant after the switch closes, here's a hint: At time t=0⁺ the switch closes and suddenly C1 and C2 are connected in parallel (all the components C1, C2, R1, R2 are in parallel when the switch is closed). What is the resulting potential on the combined capacitance? Note that the wiring is assumed to be ideal (no resistance).

 

[NascentOxygen]

When the switch is closed, the charge on C₁ "instantly" redistributes over C₁ and C₂.

 

[Ivan Antunovic]

When the switch is closed, the charge on C₁ "instantly" redistributes over C₁ and C₂.

Well since this is infinitesimally small period t = (0+) - (0-) ---->0 the voltage and therefore the charge cannot change over such a small period of a time ,since dv/dt can never be rapid atleast in particle way.And from that I conclude that there cannot be 'instantly' redistrubuted .I might be wrong on this one,just my thoughts.

Your voltage across C1 for time t=0- is fine. It's the result of the R&R1 voltage divider.

For the instant after the switch closes, here's a hint: At time t=0⁺ the switch closes and suddenly C1 and C2 are connected in parallel (all the components C1, C2, R1, R2 are in parallel when the switch is closed). What is the resulting potential on the combined capacitance? Note that the wiring is assumed to be ideal (no resistance).

Okay,I had the same picture in my head of things happening like you have mentioned.
Ceq = C1 + C2,
Q1(-0)=Q1(+0)=C1 * (E/(R1+R) * R1
Veq(+0)=Vc2(+0)=Q1(+0) / Ceq =( C1/ (C1+C2))*R1*(E/(R1+R))
I guess this should be the right solution.

 

[gneill]

Since the components are considered to be ideal there is no resistance involved in the connections joining the capacitors when the switch is closed. So the time constant pertaining to the redistribution of charge across the pair is zero. I know, one might think that is not practically possible since the charge carriers in reality have mass and so must take some time to move, but we are not looking at such ultimate physical details here in the ideal case. It is sufficient to know that any time constant involved in this process is significantly smaller (and by a very wide margin) than any other time constant involved in the circuit.

And, I presume that this is why @NascentOxygen used quotes around the word "instantly"

Hence for all practical purposes the charge distributes itself instantly across both capacitors.

Veq(+0)=Vc2(+0)=Q1(+0) / Ceq =( C1/ (C1+C2))*R1*(E/(R1+R))
I guess this should be the right solution.

Looks good.

 

[Ivan Antunovic]

Since the components are considered to be ideal there is no resistance involved in the connections joining the capacitors when the switch is closed. So the time constant pertaining to the redistribution of charge across the pair is zero. I know, one might think that is not practically possible since the charge carriers in reality have mass and so must take some time to move, but we are not looking at such ultimate physical details here in the ideal case. It is sufficient to know that any time constant involved in this process is significantly smaller (and by a very wide margin) than any other time constant involved in the circuit.

And, I presume that this is why @NascentOxygen used quotes around the word "instantly"

Hence for all practical purposes the charge distributes itself instantly across both capacitors.

Looks good.

When replacing C1 and C2 with Ceq,I get thevenin equivalent of a circuit,where time constant is T=R*Ceq,how does a time constant pair to zero?

Edited:
Okay,I think I got it,since we are only looking for an exchange of a charge between C1 and C2 which are connected parallel without any resistance,the charge will be redistributed very fast,we actually don't care if there is a battery and a resistor on the other side?

 

[Ivan Antunovic]

When replacing C1 and C2 with Ceq,I get thevenin equivalent of a circuit,where time constant is T=R*Ceq,how does a time constant pair to zero?Am I missing something here?

 

[gneill]

The time it takes the charges to redistribute across the capacitors is not tied to the time constant of the surrounding circuit. None of those components are involved in that process -- no current has to flow through any of those resistors for this charge redistribution to happen.

 

[Ivan Antunovic]

The time it takes the charges to redistribute across the capacitors is not tied to the time constant of the surrounding circuit. None of those components are involved in that process -- no current has to flow through any of those resistors for this charge redistribution to happen.

Just edited the post above,I figured it out by myself. :)