ghostcloak
- 3
- 0
Homework Statement
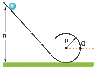
A small solid marble of mass m and radius r will roll without slipping along the loop-the-loop track, shown below, if it is released from rest somewhere on the straight section of track. For the following answers use m for the mass, r for the radius of the marble, R for the radius of the loop-the-loop and g for the acceleration due to gravity.
Here's the picture:
From what minimum height h above the bottom of the track must the marble be released to ensure that it does not leave the track at the top of the loop?
Homework Equations
Centripetal Acceleration = mg
Ki+mgh=Kf+mg(2R)
The Attempt at a Solution
Centripetal Acceleration = mg
Centripetal Acceleration = (mv^2)/R
(mv^2)/R = mg
v^2 = gR
Ki+Ui=Kf+Uf
Ki = 0
Ui = mgh
Kf = (mv^2)/2
Uf = mg(2R)
mgh = (mv^2)/2 + 2mgR
gh = (v^2)/2 + 2gR
gh = gR/2 + 2gR
h = R/2 + 2R
h = (5/2)R
In my attempt at the solution, I calculated (incorrectly) that the initial height needs to be 2.5*R. However, I did visit this old thread here: https://www.physicsforums.com/showthread.php?t=6357
The answer is actually 2.7*R, which is indeed the correct answer. Can someone help me out in identifying what I did wrong?
Thank you. :)
Attachments
Last edited: