What Torque is Needed to Lift a Retracting Nose Wheel at 30 Degrees?

[gymptp]

Homework Statement

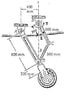
A retracting nose wheel assembly is raised by the application of a Torque T applied to link BC through a shaft at B. The wheel and arm AO have a combined mass of 50kg with a centre of mass at G. Find the value of T necessary to lift the wheel when D is directly under B at which position angle theta is 30 degrees.

Homework Equations

Nil

The Attempt at a Solution

Having difficulties getting started. Would like some assistance to get started. Feeling very lost at the moment.

 

[minger]

Well, the torque applied to arm BC is going to cause a force tangent to the arm at C, with a magnitude of torque*length_arm. A component of that force will travel along arm CD. You now have a force at point D, with a vector pointing towards C.

From here, you break 'that' force into components, one is acting radially AG, one is acting tangentially. That force*length_AD must be greater than the torque that the masses create around point A.

If it's me, I first see what force at D is needed to overcome the mass. Then I see what force along arm CD is needed to get that particular component. Then backwards again through BC.