Whats The answer and reason of this?

  • Thread starter Thread starter sufyanu
  • Start date Start date
  • Tags Tags
    Reason
AI Thread Summary
The discussion revolves around calculating the net capacitance between points A and B for a configuration of 2µF capacitors. Participants emphasize the importance of correctly applying the formulas for series and parallel combinations of capacitance. The user is encouraged to identify the simplest combinations to facilitate the calculation. Additionally, there is a suggestion to revisit and correct any inaccuracies in the formulas used. The conversation highlights the need for a clear understanding of capacitor arrangements to arrive at the correct answer.
sufyanu
Messages
2
Reaction score
0
Hi there i was thinking about this question but i can't get the solution for solving it

The question is:-
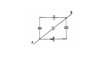
A number of capacitors each of 2µF are connected as shown in the figure given below:
(Please open the link below)

What is the net capacitance between A & B?

A. 2µF
B. 4µF
C. 6µF
D. 10µF
The equations for series and parallel combinations of capacitance are:
Parallel; C=1/C1+1/C2
Series; C=C1+C2

i don't know how to use these equations for getting final answer
 

Attachments

  • Presentation1.jpg
    Presentation1.jpg
    7.2 KB · Views: 419
Physics news on Phys.org
Your formulas are incorrect. After you correct those, the trick is always to look for the simplest combination to combine. Come back with some work.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating the voltage across capacitors and resistors with switches
Replies
2
Views
774
Capacitors in Series and Parallel
Replies
1
Views
4K
Struggling to find the equivalent capacitance of this circuit
Replies
11
Views
2K
Capacitors in series or in parallel? - calculating CR
Replies
8
Views
2K
Non-Complex Capacitor Potential Difference question
Replies
9
Views
2K
Energy stored in Capacitor Network
Replies
2
Views
13K
What is the value of capacitance C?
Replies
3
Views
4K
Find the unknown capacity of two capacitors
Replies
5
Views
1K
LC oscillations - two capacitors and an inductor
Replies
15
Views
589
How to find the charge on each capacitor
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top