SpringWater
- 27
- 0
I have a issue with determining when to use cos and sin when calculating torque;
For example. Referring to the attached picture. The SEESAW asks evaluate the torque of m2 (m2>>m1).
For second part evaluate the torque...
MY question:
WHY in the first part (SEESAW) do they use cos and why in the second part do they use sin? How do you determine; when to use cos or sin?
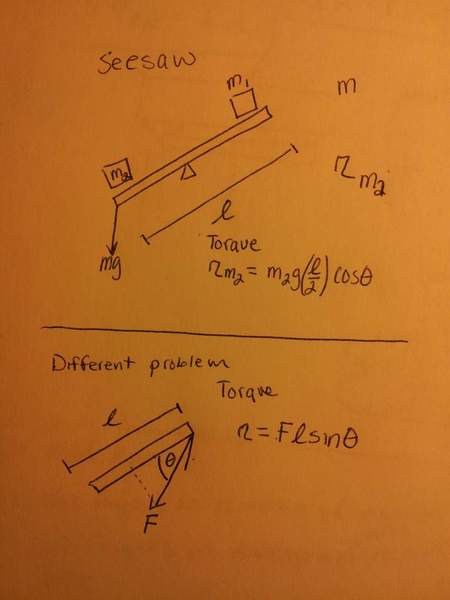
For example. Referring to the attached picture. The SEESAW asks evaluate the torque of m2 (m2>>m1).
For second part evaluate the torque...
MY question:
WHY in the first part (SEESAW) do they use cos and why in the second part do they use sin? How do you determine; when to use cos or sin?