navneet9431
Gold Member
- 107
- 9
Homework Statement
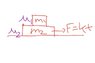
A block m2 is placed on a surface where the coefficient of friction is μ2 and another block m1 placed over the block m2 where the coefficient of frictio is μ1.
A force F=k*t(Force as a function of time),is acting on the block m2.
Now my question is that when would the block m2 start moving?
Homework Equations
F=ma
Static Friction=Coefficient Of Friction*Normal Force
The Attempt at a Solution
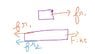
I tried solving this by drawing the FBD of the objects.
See two forces fr1 and fr2 will be acting on the block m2.
So m2 would start to move when F>fr1+fr2.
Or simply we can say k*t=fr1+ft2.
So the block m2 would start to move just after time "t".
Is my result correct?